Brechzahl
| Brechzahl | ||
|---|---|---|
| vernetzte Artikel | ||
| Konzentration | Refraktometer | |
Mit der Brechzahl (= Brechungsindex) eines Stoffes gibt man an, wievielmal langsamer sich das Licht in diesem Stoff fortbewegt als im luftleeren Raum.
Tauche einen Bleistift in ein Becherglas, welches Du zur Hälfte mit Wasser befüllst. Der Stift sieht aus, als wenn er in der Mitte einen Knick hat.
Du wirst verstehen, was die Ursache diese optische Täuschung ist, wenn Du diese Seite über den Brechungsindex durcharbeitest. Gleichzeitig erfährst Du, wie sich dieses Phänomen nutzen lässt, um unbekannte Stoffe zu identifizieren.
Inhaltsverzeichnis
Brechungsindex
Ein Lichtstrahl breitet sich strenggenommen nur im Vakuum mit der Lichtgeschwindigkeit c aus. Beim Hindurchscheinen durch transparente Stoffe wie Waser ist die Ausbreitungsgeschwindigkeit des Lichtes kleiner. Die Brechzahl (=Brechungsindex) n steht für das Verhältnis beider Geschwindigkeiten, d. h. steht für den Faktor, um den die Lichtgeschwindigkeit im Stoff cStoff kleiner ist als die im Vakuum. Als Formel:
| c | ||
| n | = | ──── |
| cStoff |
Beispiel Wasser: Der Brechungsindex von Wasser beträgt bei 20°C 1,333. Aus der o. a. Formel kann die Ausbreitungsgeschwindigkeit des Lichtes in Wasser errechnet werden:
- cWasser = c / n
- cWasser = 299.792,458 km · s–1 / 1,333
- cWasser = 224.900.569 km · s–1
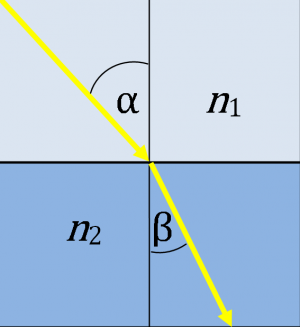
Eine alternative Berechnung der Brechzahl ergibt sich aus der Beobachtung der Lichtbrechung: Beim Übergang eines Lichtstrahles in das optisch dichtere Medium wird der Lichtstrahl zum Lot hin gebrochen, der Austrittswinkel 𝜷 ist kleiner als der Eintrittswinkel α. Für unseren Bleistift bedeutet dies, dass der Knick genauso verläuft wie der Lichtstrahl im rechten Bild. Nach Snellius gelten bei der Brechung die folgenden Zusammenhänge:
Die Sinus der Winkel verhalten sich umgekehrt zueinander wie die Brechungsindizes der Medien.
| sin α | n2 | |
| ──── | = | ──── |
| sin 𝜷 | n1 |
Da im Vakuum der Brechungsindex n1 per Definition den Wert 1 (unverminderte Geschwindigkeit) besitzt, folgt als Sonderfall aus der obigen Gleichung:
| sin α | ||
| n2 | = | ──── |
| sin 𝜷 |
Die Kenntnis dieser mathematischen Zusammenhänge ermöglichen die experimentelle Bestimmung der Brechzahl einer Probelösung, siehe Refraktometrie.
Refraktometrie
Die Messung der Brechzahl einer Flüssigkeit kann mit dem Refraktometer durchgeführt werden, das Verfahren selbst wird daher als Refraktometrie bezeichnet.
Mathematischer Hintergrund
Aus den o. a. Beziehungen ergibt sich das Messprinzip zur experimentellen Bestimmung der Brechzahl n2 einer Probelösung: Licht tritt aus einer Luftschicht in einem definierten Winkel zur Senkrechten, z. B. α = 45° in die Probe ein. Gemessen wird nun der Winkel 𝜷 in der Lösung, z. B. 30°. Über den bekannten Brechungsindex n1 der Luft (n = 1,000292) kann mittels obiger Formel auf den Brechungsindex n2 der Probe geschlossen werden:
|
|
|
|
Praktischer Nutzen
Da der Brechungsindex nicht nur eine stoffabhängige Größe ist, sondern auch mit zunehmender Konzentration einer wässrigen Lösung (Salzwasser, Zuckerlösung) ansteigt, hilft der B. bei der Identifizierung unbekannter Flüssigkeiten bzw. Konzentrationen.
Beispiele:
- Konzentration: Bei der oben untersuchten Probelösung mit dem ermittelten Brechungsindex von 1,4146 soll es sich um eine Zuckerlösung handeln. Wie lässt sich nun auf den Zuckergehalt schließen? Im einfachsten Fall hat der Hersteller des Refraktometers gleich eine entsprechende Tabelle mitgeliefert. Allerdings lassen sich solche Tabellen auch im Internet recherchieren, siehe Linkliste. Die "Zuckerverordnung der Europäischen Union" beinhaltet seitenlange Referenz-Tabellen mit Brechungsindices von Zuckerlösungen. Zum experimentell ermittelten Brechungsindex findet man hier den passenden Zuckergehalt: 47,4%.
- Brechungsindex als stoffabhängige Größe: Bestimme experimentell bzw. recherchiere den Brechungsindex für die Alkohole Methanol, Ethanol, Propan-1-ol und Butan-1-ol.
a) Erstelle aus diesen Daten ein Diagramm, welches den Zusammenhang C-Anzahl/Brechungsindex veranschaulicht.
b) Welche Abhängigkeit lässt sich erkennen?
c) Welchen Brechungsindex erwartest Du für Pentan-1-ol?
- _____________________
- Ergebnisse vergleichen
Weblinks
- Brechzahl als Google-Suchbegriff
- Brechzahl in der Wikipedia
- Brechzahl hier in bs-wiki.de mit Google
- Brechzahl als Youtube-Video
- Einführung in das Thema Brechzahl mit Übungsaufgaben und Versuchsbeschreibungen auf LEIFI, der Schulphysikseite von Ernst Leitner und Uli Finckh
- Laborpraxis: Skript von G. Rosenfeldt
- Referenz-Tabellen Brechungsindices (n) von Sucroselösungen bei 20°C
In: Erste Richtlinie 79/796/EWG der Kommission vom 26. Juli 1979 zur Festlegung gemeinschaftlicher Analysemethoden für die Kontrolle von zur menschlichen Ernährung bestimmten Zuckerarten.