Festigkeitsberechnung

Viel Spaß beim Lesen dieses Artikels, der momentan jedoch noch nicht vollständig ist...

Prolog

Mit diesem Artikel möchte ich dem Leser oder der Leserin einen sanften Einstieg in die Festigkeitsberechnung bieten, mit dem man ohne Vorkenntnisse an einfache Probleme der Festigkeitsberechnung herangehen kann, wie z.B. der Bestimmung von zulässigen Spannungen bei Schrauben oder der Handhabung von zusammengesetzten Beanspruchungen (die in mehreren Ebenen am Bauteil angreifen). Ferner möchte ich Sie mit der statischen und dynamischen Beanspruchung vertraut machen bzw. Ihnen einen kleinen Überblick verschaffen. Mein Dank gilt insbesondere den Verfassern des Roloff/Matek, an dessen Ausführungen ich mich weitgehend orientiere.

Was ist eigentlich Festigkeit?

Festigkeit ist der mechanische Widerstand eines festen Körpers, den ein Bauteil, z.B. eine Schraube oder ein Bolzen einer Belastung entgegensetzt. Diese Belastung kann elastischer oder plastischer Natur sein, d.h. nach der Belastung geht der Körper wieder in seine Ausgangslage zurück (elastisch) oder nicht (plastisch). Aus dem Spannungs-Dehnungs-Diagramm können die relevanten Festigkeitswerte (Werkstoffkennwerte) ermittelt werden. Hier kann man beispielsweise die Elastizitätsgrenze R_e ablesen. Je nach Werkstoff, Temperatur, Belastungsart und Behandlungszustand können unterschiedlich hohe Festigkeiten erreicht werden. Da die Werkstoffkennwerte im einachsigen Zugversuch ermittelt werden aber die Bauteile oft mehrachsig belastet werden (z.B. Wellen auf Biegung und Torsion), muss man eine sogenannte "Festigkeitshypothese" anwenden um eine Vergleichsspannung ermitteln, die man dann mit einer bekannten Festigkeit vergleicht.
(Anm.: "Als eine Hypothese (altgriechisch - die Unterstellung, Voraussetzung, Grundlage) bezeichnet man eine Aussage, deren Gültigkeit bloß vermutet wird, die aber ... auch begründet werden kann. Für Hypothesen ist es üblich, dass die Bedingungen angegeben werden, unter denen sie gültig sein sollen."(aus wikipedia.de))

Es gibt in der Festigkeitslehre statisch (ruhend) beanspruchte Bauteile, z.B. Schrauben oder Sicherungselemente und dynamisch (bewegt) beanspruchte Bauteile, z.B. Wellen, Achsen oder elastische Federn.
Schwingend beanspruchte Bauteile müssen nach anderen Gesichtspunkten gestaltet und berechnet werden als rein statisch beanspruchte Bauteile. Niedrige Beanspruchungen können vom Bauteil (Werkstoff) beliebig oft ertragen werden, ohne zum Versagen zu führen. Aufgabe des Konstrukteurs ist es nun, entweder die Lebensdauer bei einer gegebenen Belastung oder die ertragbare Belastung bei einer geforderten Lebensdauer zu bestimmen.

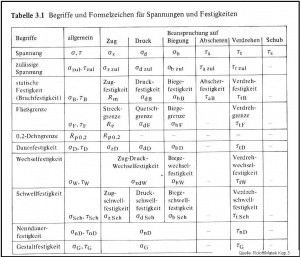
Zum Einstieg möchte ich noch einen Überblick geben über Begrifflichkeiten und Abkürzungen, die in diesem Artikel häufig verwendet werden:

Abkürzungen und Begriffe

Belastungen und Belastungsgrößen

Man unterscheidet in

• senkrecht auf eine Fläche angreifende Kraft, die Normalkraft F (Kraft in N),
  
  
• seiltich angreifende Kraft, das wäre in dem Fall ein M_b (Biegemoment in Nm),
  
  
• und einer Drehbeanspruchung, dem T (Dreh- oder Torsionsmoment in Nm).
  
  

Belastungen wirken von außen auf ein Bauteil. Dadurch kommt es nach Newton im Bauteil zu einer Gegenreaktion.
Dort entstehen dann Spannungen, d.h. es wirkt eine Kraft auf eine Fläche. Die im gefährdeten Querschnitt auftretende Spannung darf den maßgebenden zulässigen Wert nicht überschreiten. Diese zulässige Spannung ist im Wesentlichen abhängig vom Werkstoff, von der Beanspruchungs- und Belastungsart sowie der geometrischen Form des Bauteils und z.B. der Bauteiltemperatur, Eigenspannungen, Werkstofffehler, korrodierend wirkenden Umgebungsmedien oder dem Behandlungszustand. Die Dimensionierung eines Bauteils richtet sich vor allem nach der Art des möglichen Versagens, das in den meisten Fällen hervorgerufen wird durch

• unzulässig große Verformungen
  
• Gewaltbruch
  
• Dauerbruch
  
• Rissfortschreiten
  
• Instabilwerden (z.B. Knicken, Beulen)
  
• mechanische Abnutzung (z.B. Verschleiss, Abrieb)
  
• chemische Angriffe (z.B. Korrosion).
  

Der konstruktiven Auslegung eines Bauteils sind die ungünstigsten Verhältnisse zugrunde zu legen.


Welche Beanspruchungs- oder Belastungsarten sind Dir bekannt?
Antwort

Spannungen

Zug-/Druckspannungen ; Schubspannungen ; zusammengesetzte Beanspruchungen

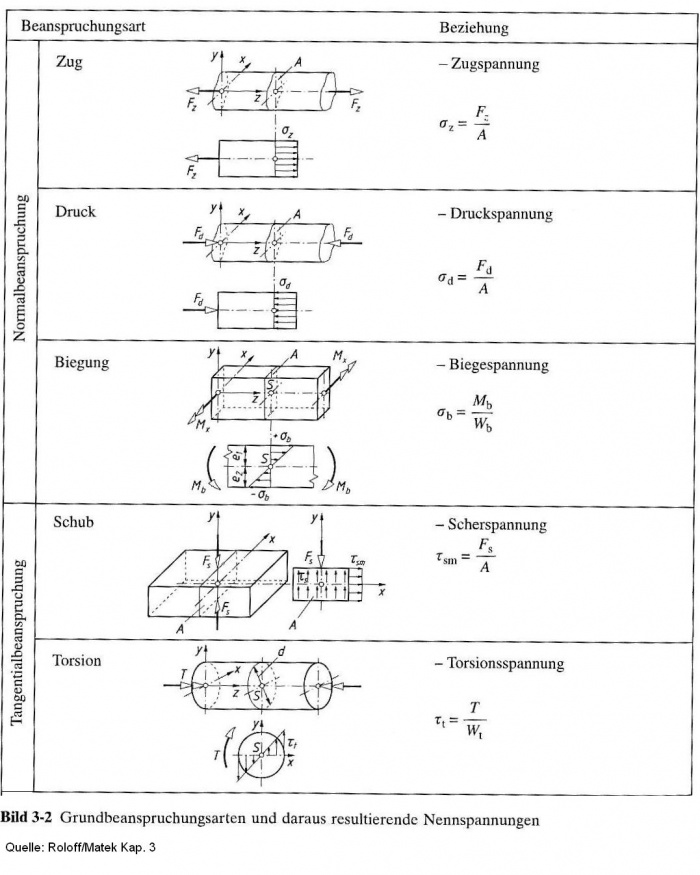
Auf das Bauteil wirken im Betrieb gewollte und ungewollte Belastungen ein. Gewollte Belastungen sind funktionsbedingt, ungewollte resultieren meist aus unerwünschten Vorgängen (Belastungsstöße, Eigenspannungen..) Im Inneren unterscheiden sich die verursachten Kraft- und Momentwirkungen in Normalkräfte F_N und Querkräfte F_Q, Biegemomente M und Torsionsmomente T. Aus ihnen ergeben sich die Beanspruchungsarten Zug, Druck, Schub, Biegung und Torsion mit den entsprechenden Nennspannungen. Senkrecht zum Bauteil werden sie als Normalspannung (Zug-, Druck-, Biegespannung), in der Querschnittsebene liegend als Tangentialspannung (Schub-, Torsionsspannung) bezeichnet.
Die entsprechenden Berechnungsformeln zu den einzelnen Beanspruchungen finden sich in der folgenden Aufstellung:

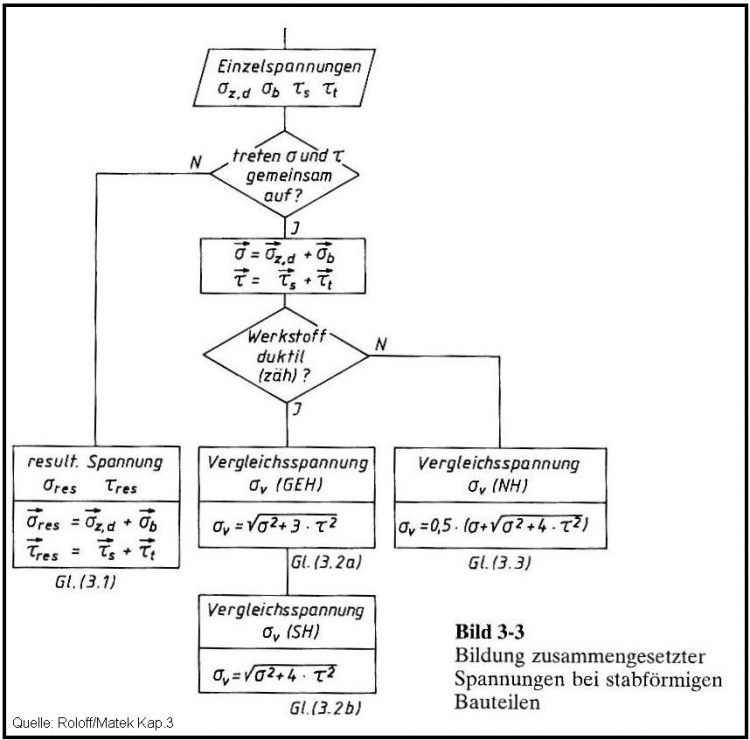
Bei zusammengesetzten Beanspruchungen liegen zwei oder mehrere Beanspruchungsarten gleichzeitig vor.
Wenn die Spannungen gleichartig sind kann eine resultierende Spannung σ_res errechnet werden.
Bei ungleicher Spannungsart wird eine Vergleichsspannung σ_v nach maßgebender Festigkeitshypothese gebildet.

noch verschieben!!

Datei:Bild 3-30neu.JPG

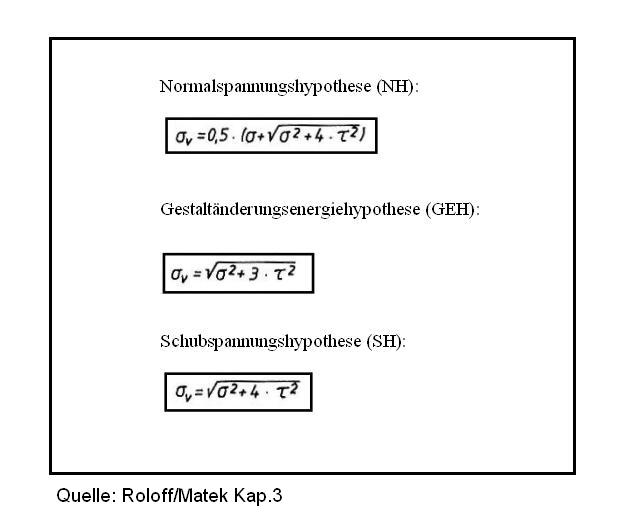
Spannungshypothesen

Die NH wird bei spröden Werkstoffen und bei Schweißverbindungen angewendet.
Die GEH wird bei duktilen (zähen) Werkstoffen angewendet.
Die SH wird bei duktilen (zähen) Werkstoffen, die überwiegend durch Torsion beansprucht werden, angewendet.

Merke: Mit Hilfe von σ_v = σ_red wird der bei einer zusammengesetzten Beanspruchung vorliegende mehrachsige Spannungszustand auf einen einachsigen Spannungszustand reduziert.(red = reduziert)

Belastungsfälle I, II und III

Je nach Art der zeitlichen Belastungsschwankung wird grundsätzlich unterschieden zwischen dem statischen und dynamischen Beanspruchungs-Zeit-Verlauf. Der statische Verlauf ist ein zeitlich konstanter Vorgang (Fall I) und der dynamische Verlauf ist allgemein zeitabhängig. Die Lage der Schwingspiele bzgl. der Beanspruchungs-Nulllinie ist für eine eindeutige Aussage hinsichtlich des Beanspruchungs-Zeit-Verlaufes von Bedeutung. Fall II beschreibt die schwellende Belastung. Beanspruchungen, deren Amplituden durch die Nulllinie verlaufen, werden als Wechselbeanspruchung (Fall III) bezeichnet. Für die Beschreibung der Beanspruchungs-Zeit-Verläufe wird von einem Schwingspiel ausgegangen, das durch folgende Kenngrößen beschrieben wird: Mittelspannung σ_m, Oberspannung σ_o, Unterspannung σ_u, Spannungsamplitude σ_a

Datei:Bild 3-1neu.GIF

Werkstoffkennwerte

Grundlage für die Ermittlung des Werkstoffgrenzwertes und der Bauteilsicherheit ist die Kenntnis über das Werkstoffverhalten bei Belastung. Im Anwendungsbereich des Maschinenbaus sind die Zugfestigkeit R_m, und die Elastizitätsgrenze R_e bzw. Rp_0,2 die Bemessungsgrößen, auf die die zugehörigen Festigkeitswerte für Zug/Druck und Schub bezogen werden. Das Werkstoffverhalten bei der Schwingbeanspruchung wird durch die tatsächliche Spannungsverteilung in einem Bauteilquerschnitt bestimmt. Durch dauernde, zu starke Spannungserhöhungen infolge geometrischer Kerben kommet es wg. ungleichmäßiger Spannungsverteilung zu einem allmählichen Ermüden des Werkstoffs. Der Trennwiderstand des Werkstoffes ist den Spannungsspitzen nicht mehr gewachsen, es kommt zu Mikrorissen, die schließlich Ursache des Dauerbruches sind. Dieser Vorgang lässt sich häufig an den Rastlinien auf der Dauerbruchfläche erkennen, ausgehend von den Mikrorissen pflanzt sich das Einreißen mit jeder höheren Belastungsspitze weiter fort. Der endgültige Bruch erfolgt als Gewaltbruch des Restquerschnitts (Restbruch).

Darstellung einer Bruchfläche

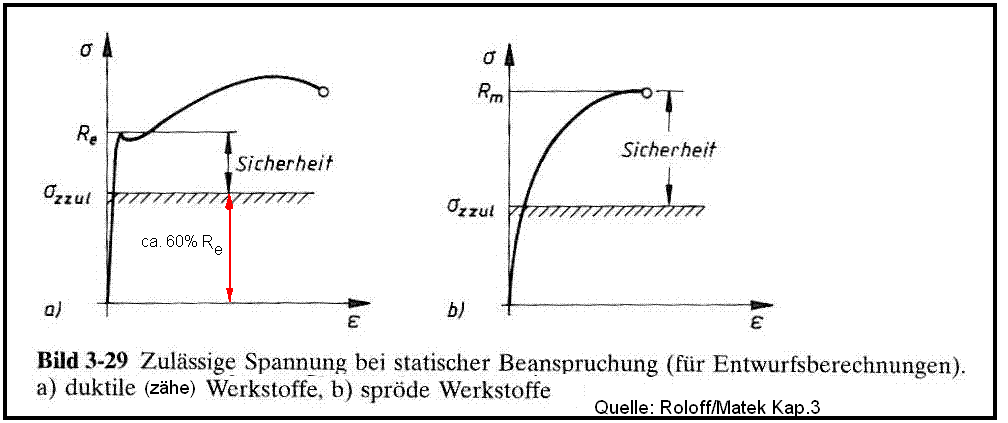
Zulässige Spannungen und erforderliche Sicherheiten

Aus Sicherheitsgründen dürfen Bauteile nur mit einem Teil der zum Bruch oder der zu bleibenden Verformung führenden Grenzspannung belastet werden.
Im Allgemeinen wird als Belatungsgrenze die Elastizitästgrenze R_e benutzt.
Im folgenden Beispiel wird die zulässige Zugspannung σ_zzul für eine Schraube M12 x 50 - 10.9 gesucht,
wenn bei statischer Belastung Sicherheit S = 2 gefordert ist:
Die Festigkeitswerte für Schrauben können dem Europa-Tabellenbuch entnommen werden!

R_e= 10 * 9 * 100 N/mm² = 900 N/mm²
σ_zzul= R_e / S = 900 N/mm² / 2 = 450 N/mm²

Abkürzungen siehe Tabelle unter 2

Festigkeits- / Sicherheitsnachweis

Allgemein gilt: (σ, τ)_vorh ≤ (σ, τ)_zul
Falls diese Bedingung nicht gegeben sein sollte ist das Bauteil größer zu dimensionieren oder es ist ein anderer Werkstoff zu wählen.
Anstatt des Festigkeitsnachweises kann auch ein Sicherheitsnachweis geführt werden:
Dort gilt allgemein: S_vorh ≤ S_erf


Wovon hängt die Festigkeit von Bauteilen ab?
Antwort

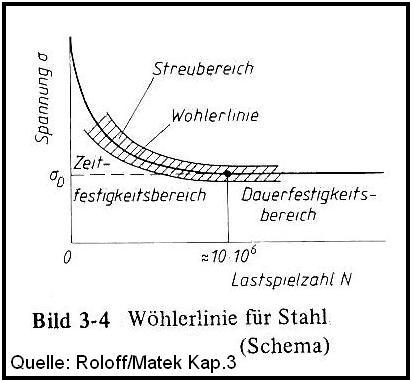
Wöhlerkurve

Die Wöhlerlinie wird auch Grenzspannungslinie genannt, sie und der Wöhlerversuch bzw. Dauerschwingversuch sind Begriffe aus der Werkstofftechnik. Sie ist benannt nach A. Wöhler, der zwischen 1858 und 1870 die ersten methodischen Schwingfestigkeitsversuche durchführte, um sich an die Grenzen der Belastbarkeit von Stahl heranzutasten.
Mit dem Wöhlerversuch wird die Schwingfestigkeit von Werkstoffen oder Bauteilen ermittelt. Hierfür werden die Versuchskörper in bestimmten zeitlichen Abschnitten belastet.
Zur Ermittlung der Werte werden die Versuchskörper auf mehreren Lasthorizonten geprüft. Der Versuch läuft, bis ein definiertes Versagen (Bruch, Anriss) eintritt oder eine festgelegte Grenzschwingspielzahl, z.B. 10⁷ erreicht wird. Versuchskörper, die die Grenzschwingspielzahl ohne erkennbares Versagen erreichen, gelten als dauerfest.

Unterhalb der Dauerfestigkeit σ_D kann ein Bauteil prinzipiell beliebig viele Schwingspiele ertragen. Belastungen oberhalb der Dauerfestigkeit bewirken ein Versagen des Bauteils nach einer bestimmten Zahl an Schwingspielen. Die Zahl der ertragenen Schwingspiele eines Bauteils unter Betriebsbelastung (variable Belastungsamplituden) bis zum Ausfall kann im Rahmen statistischer Genauigkeit mit Hilfe der Wöhlerlinie vorausgesagt werden. Man spricht hierbei von betriebsfester Bemessung eines Bauteils. Betriebsfestigkeit wird heute in nahezu allen Bereichen der Technik zum Zweck des Leichtbaus eingesetzt.

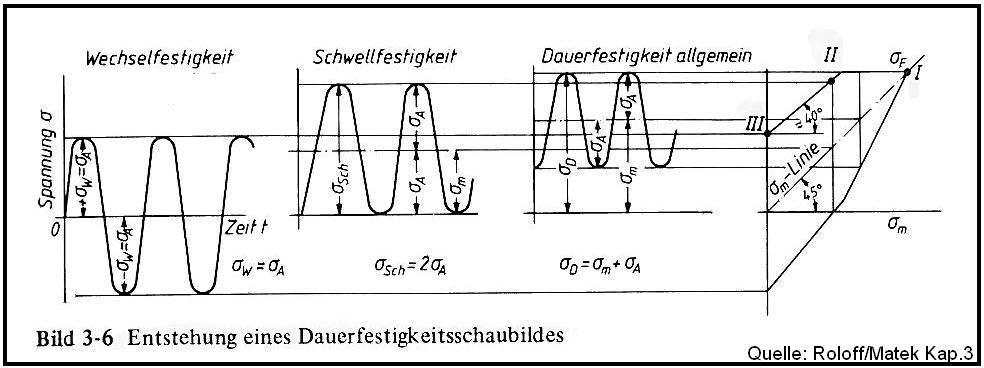
Dauerfestigkeitsschaubild (DFS)

Für die verschiedenen Beanspruchungsarten werden die ermittelten Dauerfestigkeitswerte in Dauerfestigkeitsschaubildern für alle denkbaren Vorspannungen (σ_m, τ_m) eingetragen. Eine genaue Darstellung solcher Schaubilder setzt eine Vielzahl statistisch abgesicherter Wöhlerlinien und somit einen großen experimentellen Aufwand voraus. Mit ausreichender Genauigkeit lässt sich ein DFS aus wenigen charakteristischen Werkstoffkennwerten näherungsweise „konstruieren“. In der Praxis wird im allgemeinen Maschinenbau zumeist mit dem DFS nach Smith gearbeitet.
DFS nach Smith:
Bei gleichem Maßstab von Abszisse und Ordinate werden die zu einer bestimmten Mittelspannung σ_m gehörenden Werte von σ_O und σ_U für die jeweils gefundene Ausschlagfestigkeit σ_A aufgetragen. Bei σ_m = 0 (κ = -1) wird die Wechselfestigkeit σ_W und bei σ_U = 0 (κ = 0 ) die Schwellfestigkeit σ_Sch abgelesen. In Höhe der Fließgrenze wird das DFS begrenzt.

Datei:Kappa1.JPG

Grenzspannungsverhältnis

Aufgabe:
Konstruiere das Dauerfestigkeitsschaubild nach Smith für den Werkstoff E335 im Maßstab 50 N/mm² = 1 cm.
gegebene Werte sind:
a) σ_m = 100 N/mm²
b) σ_m = 200 N/mm²
c) σ_m = 470 N/mm²
R_m = 590 N/mm²; R_e = 335 N/mm²
gesucht wird die Ausschlags-, die Ober- und die Unterspannung.

Lösung

Beispielaufgaben

Aufgabe 1: Zugkraft und -spannung bei einer Fahrradbremse
Aufgabe 2: Vergleichsspannung bei einem Fahrrad-Kurbeltrieb
Aufgabe 3: Zugbelastung

Und hier geht es zu den Lösungen:

Lösungen

Quellen

Roloff/Matek: Maschinenelemente, Lehrbuch und Tabellenbuch, Vieweg Verlag, 18. Aufl. 2007, ISBN 3-834-80262-X , € 36,90.
Roloff/Matek Maschinenelemente Formelsammlung, Vieweg Verlag, 8. Aufl. 2006. ISBN 3-834-80119-4, € 20,90.
Roloff/Matek: Maschinenelemente, Lehrbuch, Vieweg Verlag, 11. Aufl. 1987
Europa Tabellenbuch Metall, 43. Auflage
Maschinentechnik, Klett Verlag, 1 Auflage
M. Blesse 05. Okt. 2008