Zugversuch: Unterschied zwischen den Versionen
Dg (Diskussion | Beiträge) (→Spannungs-Dehnungs-Diagramm und Werkstoffkenngrößen bei der Belastung auf Zug) |
Dg (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
{{navi|Zugfestigkeit|Stahl}} | {{navi|Zugfestigkeit|Stahl}} | ||
| + | [[Bild:Zugversuch.jpg|right|Universalprüfmaschine]] | ||
| + | == Bedeutung == | ||
| − | |||
| − | |||
Der Zugversuch ist einer der wichtigsten Versuche in der Werkstoffprüfung. | Der Zugversuch ist einer der wichtigsten Versuche in der Werkstoffprüfung. | ||
Mit diesem Prüfverfahren werden Festigkeitskennwerte und Verformungskennwerte wie [[Streckgrenze]], [[Zugfestigkeit]] und [[Bruchdehnung]] bestimmt. | Mit diesem Prüfverfahren werden Festigkeitskennwerte und Verformungskennwerte wie [[Streckgrenze]], [[Zugfestigkeit]] und [[Bruchdehnung]] bestimmt. | ||
Version vom 11. Dezember 2009, 22:02 Uhr
| Zugversuch | ||
|---|---|---|
| vernetzte Artikel | ||
| Zugfestigkeit | Stahl | |
Inhaltsverzeichnis
Bedeutung
Der Zugversuch ist einer der wichtigsten Versuche in der Werkstoffprüfung. Mit diesem Prüfverfahren werden Festigkeitskennwerte und Verformungskennwerte wie Streckgrenze, Zugfestigkeit und Bruchdehnung bestimmt. Diese Werkstoffkenngrößen sind die Grundlage für die Dimensionierung statisch beanspruchter Bauteile.
Im Zugversuch wird das Werkstoffverhalten bei stetig zunehmender Zugbeanspruchung untersucht, d. h. die fest eingespannte Zugprobe wird in einer hydraulischen Zerreißmaschine ("Universalprüfmaschine", Zugprüfmaschine") stoßfrei und gleichmäßig gedehnt, bis ein Bruch eintritt.
Gleichzeitig wird eine für den Werkstoff charakteristische Kennlinie, das sogenannte Spannungs-Dehnungs-Diagramm aufgenommen.
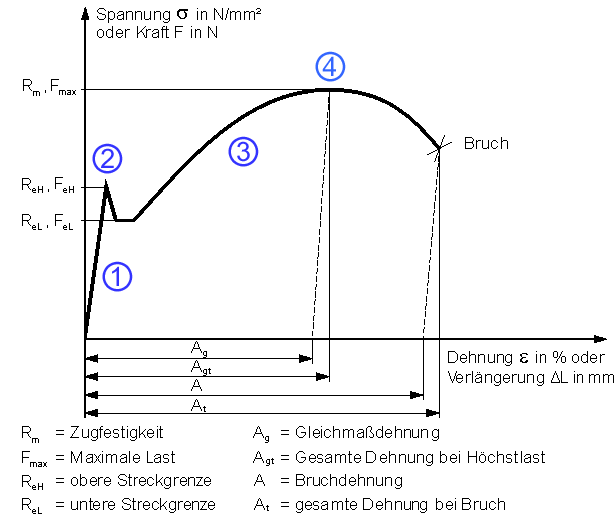
Spannungs-Dehnungs-Diagramm und Werkstoffkenngrößen bei der Belastung auf Zug
Das Spannungs-Dehnungs-Diagramm bzw. Kraft-Verlängerungs-Diagramm dient zur Bestimmung der Festigkeits- und Verformungskenngrößen bei der Belastung eines Werkstoffes auf Zug. Bedeutsam sind die folgenden Bereiche:
- Elastische Verformung: Zu Beginn der Lastaufbringung erfolgt die Dehnung der Probe elastisch, d. h. nach Entlastung nimmt der Stab seine Ausgangslänge L0 wieder ein. Im Diagramm stellt sich dieser Bereich als Gerade dar. Spannung und Dehnung ändern sich verhältnisgleich. Diesen Zusammenhang erkannte erstmals der Physiker Hooke, nach dem dieser Bereich auch Hookescher Bereich des Werkstoffs genannt wird.
- Streckgrenze: Die Streckgrenze Re ist die Grenze zwischen elastischer und plastischer Verformung. Im Spannungs-Dehnungs-Diagramm ist sie oberhalb der Hookeschen Gerade als markanter Wendepunkt zu erkennen, da beim Überschreiten der Zusammenhangskräfte zwischen den Atomen der Werkstoff „zu fließen“ beginnt, d.h. sich plötzlich schneller verformt, als dies bei entsprechender Steigerung der Zugbelastung zu erwarten wäre. Als Grenzwert für die Dimensionierung von Bauteilen gilt stets die Streckgrenze, da bei plastischer Verformung das Werkstoffgefüge zerstört wird!
- Plastische Verformung: Bauteil bleibt dauerhaft verformt, ist aber augenscheinlich nicht zerstört.
- Reißen / Bruch, die Zugfestigkeit (Rm) ist die max. Belastung vor dem Reißen.
Beispiel
Im Zugversuch wird ein Probestab auf Zug bis zum Zerreißen belastet. Bei einem Anfangsdurchmesser von 10 mm wird eine Zerreißkraft von 25.000 N ermittelt.
- Wie groß ist der belastete Spannungquerschnitt?
- Welche Zugfestigkeit besitzt der Probestab?
1. Berechnung des Spannungsquerschnittes A in mm²
A = d2 · π · 0,25
A = (10 mm)2 · π · 0,25
A = 78,5 mm²
2. Berechnung der Zugfestigkeit Rm in N/mm²
Rm = FZ : A
Rm = 25.000 N : 78,5 mm²
Rm = 25.000 N : 78,5 mm²
Rm = 312,45 N/mm²
In welchem Verhältnis stehen Zugfestigkeit und Streckgrenze bei Stahl?
| Stahlsorte | S 235JR | X2 Cr Ni 12 | S 185 |
| Streckgrenze (Re) in N/mm² | 235 | 260 | 185 |
| Zugfestigkeit (Rm) in N/mm² | 340...470 | 450...600 | 290...510 |
| Mittelwert in N/mm² | 405 | 525 | 400 |
| Rm/Re | 1,72 | 2,02 | 2,16 |
Die Streckgrenze beträgt also nur ca. die halbe Zugfestigkeit!
Übung
Eine Schraube mit 30 mm Durchmesser wird auf Zug belastet. Wie groß ist die belastete Fläche?
Lösung:
Zugversuch: Lösung