Elastizitätsmodul: Unterschied zwischen den Versionen
Dg (Diskussion | Beiträge) (→Elastizitätsmoduln) |
Dg (Diskussion | Beiträge) |
||
| (35 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{navi|Streckgrenze|Stahl}} | {{navi|Streckgrenze|Stahl}} | ||
| − | Elastizität ist die Eigenschaft fester Stoffe, nach einer Verformung (z.B. Verlängerung während einer Belastung auf Zug) wieder in ihren ursprünglichen Zustand überzugehen. | + | == Elastizität und Elastizitätsmodul == |
| + | [[Bild:Schlauch.jpg|thumb|right|600px|Ein leicht dehnbarer Gummischlauch hat einen kleinen Elastizitätsmodul.]] | ||
| + | [[Bild:Spannungsdehnungsdiagramm.gif|right]] | ||
| + | '''Elastizität''' ist die Eigenschaft fester Stoffe, nach einer Verformung (z.B. Verlängerung während einer Belastung auf Zug) wieder in ihren ursprünglichen Zustand überzugehen. | ||
| − | + | Der '''Elastizitätsmodul''' (kurz: E-Modul, ''E'') beschreibt die Elastizität von Werkstoffen [[quantitativ]] ("Hookesches Gesetz"). Hierbei gilt: {{mark|Je elastischer der Stoff, desto kleiner der E-Modul.}} | |
| − | + | === Experimentelle Bestimmung des Elastizitätsmoduls === | |
| + | Der Elastizitätsmodul kann über den [[Zugversuch]] [[experiment]]ell bestimmt werden: | ||
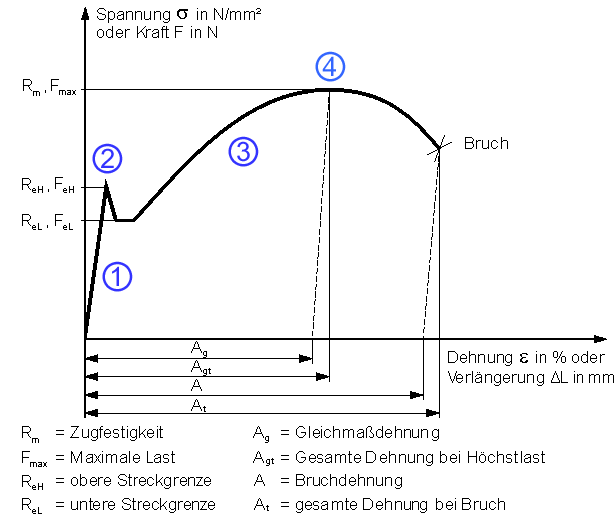
| − | + | Im elastischen Bereich (siehe [[Spannungs-Dehnungs-Diagramm]] (1, [[Hookesche Gerade]]) wird das Verhältnis der [[Zugspannung]] ''σ<sub>Z</sub>'' (= Zugkraft ''F<sub>Z</sub>'' pro Querschnittfläche ''S'') zur [[Dehnung|Längsdehnung ''ε'']] ermittelt, dieses Verhältnis ist der E-Modul in N/mm<sup>2</sup> bzw. bzw. Megapascal (MPa): | |
| + | {{Bruch|ist==|ZL=|BL=''E''|NL=|ZR=''[[Zugspannung|σ<sub>Z</sub>]]''{{*}}100% ''F<sub>Z</sub>''{{*}}''L<sub>0</sub>''|BR=<b>─────── = ─────</b>|NR= ''[[Dehnung|ε]]'' ''S''{{*}}''ΔL''}} | ||
| − | E = 10.000 N{{*}}200 mm / | + | == Berechnungsbeispiele == |
| + | === Experimentelle Bestimmung des Elastizitätsmoduls === | ||
| + | ''Im Zugversuch kann der E-Modul experimentell bestimmunt werden, z. B.:'' | ||
| + | Ein Probestab aus Stahl mit einer Ausgangslänge ''L<sub>0</sub>'' von 200 mm und einer Querschnittsfläche ''S'' von 78,5 mm² wird mit einer Kraft ''F<sub>Z</sub>'' von 10.000 N auf Zug belastet. Hierbei stellt sich eine Verlängerung von 0,12 mm ein. | ||
| + | |||
| + | ''E'' = 10.000 N{{*}}200 mm / 78,5 mm²{{*}}0,12 mm | ||
{{Ergebnis|E|212.314 N/mm<sup>2</sup>}} | {{Ergebnis|E|212.314 N/mm<sup>2</sup>}} | ||
| + | === Berechnung der elastischen Verlängerung eines Zugstabes === | ||
| + | ''Über den E-Modul kann die elastische Verlängerung eines Bauteils berechnet werden, z. B.:'' | ||
| + | Ein Flachstahl 4 x 30 mit der Länge 2 m wird mit 18 kN auf Zug belastet. Berechne die elastische Verlängerung. | ||
| + | {{Bruch|ist==|ZL=|BL=''ΔL''|NL=|ZR=''F<sub>Z</sub>''{{*}}''L<sub>0</sub>'' 18.000 N''{{*}}''2.000 mm{{*}}mm² |BR=<b>───── </b>=<b> ──────────────────</b> = 1,4 mm|NR=''S''{{*}}''E'' 120 mm²{{*}}210.000 N }} | ||
== Elastizitätsmoduln == | == Elastizitätsmoduln == | ||
| Zeile 17: | Zeile 31: | ||
{| {{Tabelle}} class = "sortable" | {| {{Tabelle}} class = "sortable" | ||
|- | |- | ||
| − | ! Material || E in N/mm² | + | ! Material || ''E'' in N/mm² |
|- | |- | ||
| Beton || 30.000 | | Beton || 30.000 | ||
|- | |- | ||
| − | | Gusseisen || 100.000 | + | | [[Gusseisen]] || 100.000 |
|- | |- | ||
| − | | Stahl || 210.000 | + | | [[Stahl]] || 210.000 |
|} | |} | ||
| Zeile 29: | Zeile 43: | ||
{{www}} | {{www}} | ||
* [http://www.tf.uni-kiel.de/matwis/amat/mw1_ge/kap_7/illustr/t7_1_2.html Uni Kiel: Elastizitätsmodul in Zahlen] | * [http://www.tf.uni-kiel.de/matwis/amat/mw1_ge/kap_7/illustr/t7_1_2.html Uni Kiel: Elastizitätsmodul in Zahlen] | ||
| + | * [http://www.physik.uni-mainz.de/lehramt/lehramt/Vortraege/Anleitung/DSchw_StEx.pdf Experimentelle Bestimmung des E-Moduls]. Umfassende Darstellung der physikalischen Grundlagen und variantenreiche experimentelle Bestimmung des E-Moduls von David Schwarzenberg (PDF, 226 S.). Die vergleichsweise einfache Bestimmung mittels Zugversuch ist hier ab S. 60 beschrieben. | ||
| − | [[Kategorie:Werkstofftechnik]] | + | [[Kategorie:Werkstofftechnik]][[Kategorie:Lerngebiet 12.7: Werkstoffe auswählen und prüfen]][[Kategorie:Stoffeigenschaft]] |
Aktuelle Version vom 27. August 2023, 10:30 Uhr
| Elastizitätsmodul | ||
|---|---|---|
| vernetzte Artikel | ||
| Streckgrenze | Stahl | |
Inhaltsverzeichnis
Elastizität und Elastizitätsmodul
Elastizität ist die Eigenschaft fester Stoffe, nach einer Verformung (z.B. Verlängerung während einer Belastung auf Zug) wieder in ihren ursprünglichen Zustand überzugehen.
Der Elastizitätsmodul (kurz: E-Modul, E) beschreibt die Elastizität von Werkstoffen quantitativ ("Hookesches Gesetz"). Hierbei gilt: Je elastischer der Stoff, desto kleiner der E-Modul.
Experimentelle Bestimmung des Elastizitätsmoduls
Der Elastizitätsmodul kann über den Zugversuch experimentell bestimmt werden:
Im elastischen Bereich (siehe Spannungs-Dehnungs-Diagramm (1, Hookesche Gerade) wird das Verhältnis der Zugspannung σZ (= Zugkraft FZ pro Querschnittfläche S) zur Längsdehnung ε ermittelt, dieses Verhältnis ist der E-Modul in N/mm2 bzw. bzw. Megapascal (MPa):
| σZ · 100% FZ · L0 | ||
| E | = | ─────── = ───── |
| ε S · ΔL |
Berechnungsbeispiele
Experimentelle Bestimmung des Elastizitätsmoduls
Im Zugversuch kann der E-Modul experimentell bestimmunt werden, z. B.: Ein Probestab aus Stahl mit einer Ausgangslänge L0 von 200 mm und einer Querschnittsfläche S von 78,5 mm² wird mit einer Kraft FZ von 10.000 N auf Zug belastet. Hierbei stellt sich eine Verlängerung von 0,12 mm ein.
E = 10.000 N · 200 mm / 78,5 mm² · 0,12 mm
E = 212.314 N/mm2
Berechnung der elastischen Verlängerung eines Zugstabes
Über den E-Modul kann die elastische Verlängerung eines Bauteils berechnet werden, z. B.:
Ein Flachstahl 4 x 30 mit der Länge 2 m wird mit 18 kN auf Zug belastet. Berechne die elastische Verlängerung.
| FZ · L0 18.000 N · 2.000 mm · mm² | ||
| ΔL | = | ───── = ────────────────── = 1,4 mm |
| S · E 120 mm² · 210.000 N |
Elastizitätsmoduln
| Material | E in N/mm² |
|---|---|
| Beton | 30.000 |
| Gusseisen | 100.000 |
| Stahl | 210.000 |
Weblinks
- Elastizitätsmodul als Google-Suchbegriff
- Elastizitätsmodul in der Wikipedia
- Elastizitätsmodul hier in bs-wiki.de mit Google
- Elastizitätsmodul als Youtube-Video
- Uni Kiel: Elastizitätsmodul in Zahlen
- Experimentelle Bestimmung des E-Moduls. Umfassende Darstellung der physikalischen Grundlagen und variantenreiche experimentelle Bestimmung des E-Moduls von David Schwarzenberg (PDF, 226 S.). Die vergleichsweise einfache Bestimmung mittels Zugversuch ist hier ab S. 60 beschrieben.