Planetengetriebe: Bauarten: Unterschied zwischen den Versionen
Silke (Diskussion | Beiträge) (→<u>'''Geschichte'''</u>) |
Silke (Diskussion | Beiträge) (→<u>'''Funktion'''</u>) |
||
| Zeile 41: | Zeile 41: | ||
=== <u>'''Funktion'''</u> === | === <u>'''Funktion'''</u> === | ||
| + | [[Bild:Ravingneaux.jpg|300px|right|Ravigneaux-Planetenradsatz <br />Quelle: Arbeitsheft Seite 29]] | ||
Die langen Planetenräder sind im Ravigneaux-Satz mit dem großen Sonnenrad und den | Die langen Planetenräder sind im Ravigneaux-Satz mit dem großen Sonnenrad und den | ||
| Zeile 48: | Zeile 49: | ||
z.B. im 3- und 4-Gang-Automatikgetriebe. | z.B. im 3- und 4-Gang-Automatikgetriebe. | ||
| − | |||
[http://www.youtube.com/watch?v=VcqoLoOWOI0] Video Funktion Ravigneaux-Planetenradsatz | [http://www.youtube.com/watch?v=VcqoLoOWOI0] Video Funktion Ravigneaux-Planetenradsatz | ||
Version vom 16. April 2009, 12:32 Uhr
| Planetengetriebe: Bauarten | ||
|---|---|---|
| vernetzte Artikel | ||
| Planetengetriebe: Aufbau und Funktion | x | |
Inhaltsverzeichnis
Simpson-Planetenradsatz
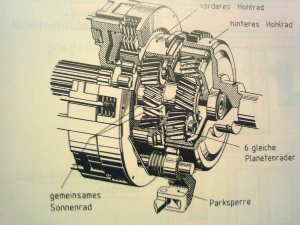
Kennzeichen
- 1 gemeinsames Sonnenrad
- 6 gleich große Planetenräder
- 2 getrennte Hohlräder
Funktion
Beim Simpson-Satz ist der Planetenradträger des einen Satzes mit dem Hohlrad des Anderen verbunden. Es können 3 Vorwärtsgänge und ein Rückwärtsgang geschaltet werden z.B. 4-Gang-Automatikgetriebe mit einem zusätzlichen Planetenradsatz.
Geschichte
- Thomas Simpson wurde am 20.08.1710 als Sohn eines Webers geboren und brachte sich die Mathematik durch Selbststudium bei.
- Er unterrichtete Mathematik
- Durch seine Arbeiten über Interpolation und numerische Integration wurde er bekannt.
- Es wurde die Simpson'sche Formel nach ihm benannt.
[1]Simpson'sche Formel
[2]Interpolation
[3]Numerische Integration
Ravigneaux-Planetenradsatz
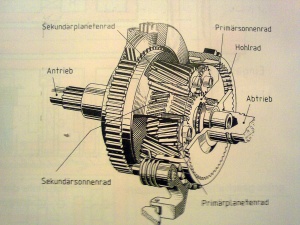
Kennzeichen
- 1 kleines und 1 zusätzliches großes Sonnenrad
- 3 lange und 3 kurze Planetenräder
- 1 Hohlrad
Funktion
Die langen Planetenräder sind im Ravigneaux-Satz mit dem großen Sonnenrad und den Planetenrädern des kleinen Sonnenrads gleichzeitig im Eingriff. Die Besonderheit dieses Satzes ist der gemeinsame Planetenträger, wodurch eine kompakte Bauweise ermöglicht wird. Es können 3 Vorwärtsgänge und ein Rückwärtsgang geschaltet werden z.B. im 3- und 4-Gang-Automatikgetriebe.
[4] Video Funktion Ravigneaux-Planetenradsatz
Geschichte
Wir haben über den Erfinder Ravigneaux leider nichts finden können.
Wilson-Satz
Aus 3 einfachen, hintereinander geschalteten Planetenradsätzen wird der Wilson-Satz gebildet. Er wird im 5 Gang-Automatik-Getriebe verwendet.
Lepelletier-Satz
Aus einem einfachen, vorgeschalteten Planetenradsatz und einem nachgeschalteten Ravigneaux-Satz, bildet sich der Lepelletier-Satz. Er wird im 6 Gang-KFZ-Getriebe verwendet.
Interne Links
Planetengetriebe: Aufbau und Funktion
Daniela und Silke