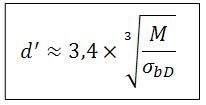Achsen, Wellen und Zapfen: Unterschied zwischen den Versionen
Teddy (Diskussion | Beiträge) (→Literatur :) |
Teddy (Diskussion | Beiträge) (→Übungsaufgabe) |
||
| Zeile 178: | Zeile 178: | ||
[[ Achsen,Wellen und Zapfen:Lösungen#Aufgabe_3|Lösung]] | [[ Achsen,Wellen und Zapfen:Lösungen#Aufgabe_3|Lösung]] | ||
<br /> | <br /> | ||
| − | <br /> | + | [[Media:Achsen_Wellen_Aufgabenblatt.pdf|Druckversion der Aufgabe]]<br /> |
<br /> | <br /> | ||
Version vom 11. Oktober 2008, 16:17 Uhr
Achsen, Wellen und Zapfen begegnen uns überall im Alltag. Am Rasenmäher, der Schubkarre, am Bobby-Car der Kinder, bei der Modelleisenbahn oder in anderen Dimensionen die Antriebswelle der Ozeanriesen.
|
Funktion und Wirkung
Achsen
Achsen sind zum Tragen und Lagern von Laufrädern, Seilrollen, Hebel etc..
Sie übertragen kein Drehmoment.
Sie werden durch Querkräfte auf Biegung, weniger durch Längskräfte zusätzlich noch auf Zug oder Druck beansprucht.
Achsen werden unterteilt in:
- feststehende Achsen
- umlaufende Achsen
Feststehende Achsen:
Auf feststehenden Achsen drehen sich die Teile (z.B. Seilrollen) lose.
Wegen der nur ruhend oder schwellend auftretenden Biegung beanspruchungsmäßig günstig.
Umlaufende Achsen:
Auf ihnen sitzen die Bauteile (z.B. Laufräder) fest.
Umlaufende Achsen werden wechselnd auf Biegung beansprucht, daher ist ihre Tragfähigkeit geringer als bei feststehenden Achsen.
Bei umlaufenden Achsen ist eine leichte Wartung der Lager möglich.
Wellen
Wellen drehen sich um ihre eigene Achse und übertragen das Drehmoment auf Zahnräder, Riemenscheiben usw.
Wellen werden auf Torsion und durch Querkräfte zusätzlich auf Biegung beansprucht.
Durch Kegelräder/schrägverzahnte Stirnräder werden zusätzliche Längskräfte in Wellen eingeleitet.
Es gibt zwei Sonderausführungen von Wellen:
Gelenkwellen werden eingesetzt um die Drehbewegung zwischen nicht fluchtenden und in ihrer Lage veränderlichen Wellenteilen zu übertragen. Sie werden im Werkzeugmaschinenbau und im Kraffahrzeugbau eingesetzt.
Aufbau:
Gelenkwellen bestehen aus mehren Teilen, der Antriebswelle, den beiden Einfach-Gelenken und einer Teleskopwelle.
Biegsame Wellen
Biegsame Wellen dienen zum Antrieb von Maschinen mit kleiner Leistung, die keinen festen Standort haben. Dies sind z.B. Handschleifmaschinen und Handfräsen.
Sie werden auch eingesetzt bei ortsfesten Geräten, bei denen ein starker Versatz zum Antrieb besteht. Das ist z.B. bei einem Tacho der Fall.
Aufbau:
Biegsame Wellen bestehen aus schraubenförmig in mehreren Lagen und mehrgängig gewickelten Stahldrähten (1), die von einem beweglichen Metallschutzschlauch (3) umgeben sind. Der Metallschlauch kann durch ein Stahlband verstärkt worden sein (2).
| Frage 1:
Welches Bauteil überträgt kein Drehmoment?
|
|---|
Zapfen
Zapfen dienen zum Tragen und Lagern von Maschinenelementen.
Sie sind meist abgesetzte Enden von Wellen und Achsen oder als Einzelelement (z.B. Kurbelzapfen) vorhanden.
Zapfen können zylindrisch, kegelig oder kugelförmig ausgebildet sein.
Gestalten und Entwerfen
Werden Achsen, Wellen und Zapfen entworfen, so ist ihre äußere Form abhängig von ihrer Verwendung und von den Bauteilen, die aufgenommen werden.
Gestaltungsgrundsätze zum Thema Festigkeit
Diese Regeln sollten beachtet werden:
- Gedrängte Bauweise mit kleinen Rad- und Lagerabständen.
- Dauerbruchgefahr ausschalten.
- Möglichst einfache und kostensparende Fertigung.
- Vermeidung gefährdeter Kerbstellen.
- Keil- und Passfedernuten nicht bis an die Übergänge heranführen.
- Räder und Scheiben gegen axiales Verschieben durch Distanzscheiben- oder hülsen, Stellringe und nicht durch Sicherungsringe sichern.
- Möglichst Fertigwellen verwenden.
- Feststehende Achsen gegenüber umlaufenden bevorzugen wegen der günstigeren Beanspruchungsverhältnisse.
- Lager dicht an Scheibe und Räder setzen.
Gestaltungsgrundsätze zum Thema Elastisches Verhalten
- Bei langen Wellen auf Verdrehung achten (Torsion).
- Bei hohen Drehzahlen Schwingungen des Systems beachten.
- Genaue rechnerische Ermittlung der Neigung, Durchbiegung bzw. torsionskritischen Drehzahl ist bei mehrfach abgesetzten Wellen zeitaufwändig. (Es werden Rechnerprogramme benutzt.)
- Sind steife Wellen gefordert, müssen diese kurz gestaltet oder als Hohlwellen ausgeführt werden.
- Allgemein ist eine möglichst hohe kritische Drehzahl anzustreben, mindestens 10-20% über Betriebsdrehzahl.
Kritische Drehzahl
Um eine möglist hohe kritische Drehzahl zu ereichen, müssen folgende Punkte beachtet werden:
- Die vorhandenen Lager möglichst dicht an Scheiben und Räder setzen, um die Durchbiegung klein zu halten.
- Bei hohen Drehzahlen die Wellen und Achsen sorgfältig auswuchten, um die Fliehkräfte klein zu halten.
- Bauteile, die sich auf den Wellen und Achsen befinden (wie z.B. Scheiben, Räder, Kupplungen), leicht bauen, damit sie ein kleines Massenträgheitsmoment haben.
Werkstoff
Aus wirtschaftlichen Gründen wird der Werkstoff für Achsen, Wellen und Zapfen nicht hochwertiger als unbedingt erforderlich ausgewäht. Bei besonderen Anforderungen an die Achsen und Wellen kann der Einsatz von hochwertigen Werkstoffen erforderlich werden.
| Beanspruchung | Werkstoffe |
|---|---|
| normal beanspruchte Achsen und Wellen | unlegierte Baustähle z.B. S235, S275 |
| höher beanspruchte Achsen und Wellen | Vergütungsstähle z.B. 25CrMo4, 28Mn6 |
| Beanspruchung auf Verschleiß | Einsatzstähle z.B. C15, 17CrNiMo6 |
| Frage 2:
Was sollte man tun um eine möglichst hohe kritsche Drehzahl zu erreichen?
|
|---|
Berechnunghinweise
Hier sind ein paar Hinweise, um die Übungsaufgabe leichter lösen zu können.
Überschlägige Ermittlung des Durchmessers einer Achse mit Kreisquerschnitt
d´ = Wellen- bzw. Achsdurchmeser in mm
M = Moment in Nmm / Nm
σbD = Biegedauerfestigkeit in N/mm2
Nachweis der statischen Sicherheit
SF = vorhandene Sicherheit gegen Fließen
SFmin = Mindestsicherheit gegen Fließen
σbmax = maximale Biegespannung in N/mm2
σbF = Biegefließgrenze in N/mm2
Τtmax = maximale Verdrehspannung, Torsionsspannung in N/mm2
ΤtF = Torsionsfließgrenze in N/mm2
Nachweis der dynamischen Sicherheit
SD = vorhandene Sicherheit gegen Dauerbruch
SDerf = erforderliche Sicherheit gegen Dauerbruch
σba = Biegeausschlagsspannung in N/mm2
σbGW = Biegegestaltwechselfestigkeit in N/mm2
Τta = Torsionsausschlagsspannung in N/mm2
ΤtGW = Torsionsgestaltwechselfestigkeit in N/mm2
Übungsaufgabe
Die Skizze zeigt die Lagerung der oberen Bandrolle einer Bandsäge mit D = 400 mm Durchmesser. Bei einer Antriebsleistung der Säge von P = 3 kW bei n = 750 min-1 ist aufgrund der erforderlichen Vorspannung des Sägebandes und unter Berücksichtigung der vorliegenden Betriebsverhältnisse mit einer Rollenkraft F ≈ 1 kN zu rechnen.
1)
Der Durchmesser d1 der Achse aus S235JR ist überschlägig zu ermitteln. Für die verschiebbaren Innenringe der Wälzlager (Rillenkugellager DIN 625) ist für die Achse die Toleranzklasse j5 vorzusehen.
Lösung
2)
Für den auf volle 5 mm gerundeten Achsdurchmesser d1 ist die erforderliche Sicherheit gegen Fließen SF nachzuweisen.
Lösung
3)
Für den auf volle 5 mm gerundeten Achsdurchmesser d1 ist die erforderliche Sicherheit gegen Dauerbruch SD nachzuweisen. (Übergangsradius r = 0,6 mm, Oberflächenrauheit RZ = 6,3 μm).
Lösung
Druckversion der Aufgabe
Literatur

|
Roloff/Matek: Maschinenelemente, Lehrbuch und Tabellenbuch; Vieweg Verlag, 18.Auflage, 2007, ISBN 978-3-8348-0262-0, Preis € 36,90 |

|
Roloff/Matek: Maschinenelemente, Formelsammlung; Vieweg Verlag, 9.Auflage, 2008, ISBN 978-3-8348-0534-8, Preis € 20,90 |

|
Roloff/Matek: Maschinenelemente, Aufgabensammlung; Vieweg Verlag, 14.Auflage, 2007, ISBN 978-3-8348-0340-5 , Preis € 26,00 |

|
Alfred Böge: Handbuch Maschinenbau; Vieweg Verlag, 18.Auflage, 2007, ISBN 978-3-8348-0110-4 , Preis € 69,90 |

|
Tabellenbuch Metall; Europa Lehrmittel Verlag, 44.Auflage, 2008, ISBN 978-3-8085-1724-6 , Preis € 23,80 |

|
Schierbock: Formeln und Tabellen für metalltechnische Berufe; Bildungsverlag Eins, 17.Auflage, 2007, ISBN 978-3-8239-7140-5 , Preis € 13,80 |
--Teddy 08:10, 30. Aug. 2008 (CEST)