Regression: Unterschied zwischen den Versionen
Dg (Diskussion | Beiträge) (→Regressionsgerade in Excel berechnen lassen) |
Dg (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
[[Bild:Leitfaehigkeit.jpg|right|403px]] | [[Bild:Leitfaehigkeit.jpg|right|403px]] | ||
| − | + | ||
Beim [[Experiment]]ieren soll häufig ein vermuteter Zusammenhang von zwei Größen genauer, also quantitativ untersucht werden. Im einfachsten Fall besteht ein linearer Zusammenhang zwischen beiden Größen, der durch das Verfahren der linearen Regression herausgearbeitet werden kann. Am Beispiel der [[Leitfähigkeitsmessung]] einer Salzlösung soll diese Vorgehensweise erklärt werden: | Beim [[Experiment]]ieren soll häufig ein vermuteter Zusammenhang von zwei Größen genauer, also quantitativ untersucht werden. Im einfachsten Fall besteht ein linearer Zusammenhang zwischen beiden Größen, der durch das Verfahren der linearen Regression herausgearbeitet werden kann. Am Beispiel der [[Leitfähigkeitsmessung]] einer Salzlösung soll diese Vorgehensweise erklärt werden: | ||
| Zeile 10: | Zeile 10: | ||
=== Durchführung === | === Durchführung === | ||
Die Leitfähigkeit der Salzlösung wird durch die Messung der Stromstärke bestimmt (Aufbau s. Bild bzw. [[Media:Leitfaehigkeit.pdf|Versuchsanleitung]]). Es wird vermutet, dass die Stromstärke mit zunehmender Salzmenge größer wird. | Die Leitfähigkeit der Salzlösung wird durch die Messung der Stromstärke bestimmt (Aufbau s. Bild bzw. [[Media:Leitfaehigkeit.pdf|Versuchsanleitung]]). Es wird vermutet, dass die Stromstärke mit zunehmender Salzmenge größer wird. | ||
| − | + | [[Bild:Regression.png|right]] | |
=== Messwerte === | === Messwerte === | ||
Alle Messwerte werden zunächst tabellarisch zusammengestellt. Als Diagramm ergibt sich hieraus eine ''Punktwolke''. Ziel der Regression ist es, eine ''Ausgleichsgerade'' durch die Punktwolke zu legen, deren Abstand zu den in der Praxis aufgenommenen Messwerten möglichst klein ist. | Alle Messwerte werden zunächst tabellarisch zusammengestellt. Als Diagramm ergibt sich hieraus eine ''Punktwolke''. Ziel der Regression ist es, eine ''Ausgleichsgerade'' durch die Punktwolke zu legen, deren Abstand zu den in der Praxis aufgenommenen Messwerten möglichst klein ist. | ||
Version vom 20. November 2012, 17:22 Uhr
Beim Experimentieren soll häufig ein vermuteter Zusammenhang von zwei Größen genauer, also quantitativ untersucht werden. Im einfachsten Fall besteht ein linearer Zusammenhang zwischen beiden Größen, der durch das Verfahren der linearen Regression herausgearbeitet werden kann. Am Beispiel der Leitfähigkeitsmessung einer Salzlösung soll diese Vorgehensweise erklärt werden:
Inhaltsverzeichnis
Praxisbeispiel
Leitfrage
Welchen Einfluss hat der Salzgehalt auf die elektrische Leitfähigkeit der Salzlösung?
Durchführung
Die Leitfähigkeit der Salzlösung wird durch die Messung der Stromstärke bestimmt (Aufbau s. Bild bzw. Versuchsanleitung). Es wird vermutet, dass die Stromstärke mit zunehmender Salzmenge größer wird.
Messwerte
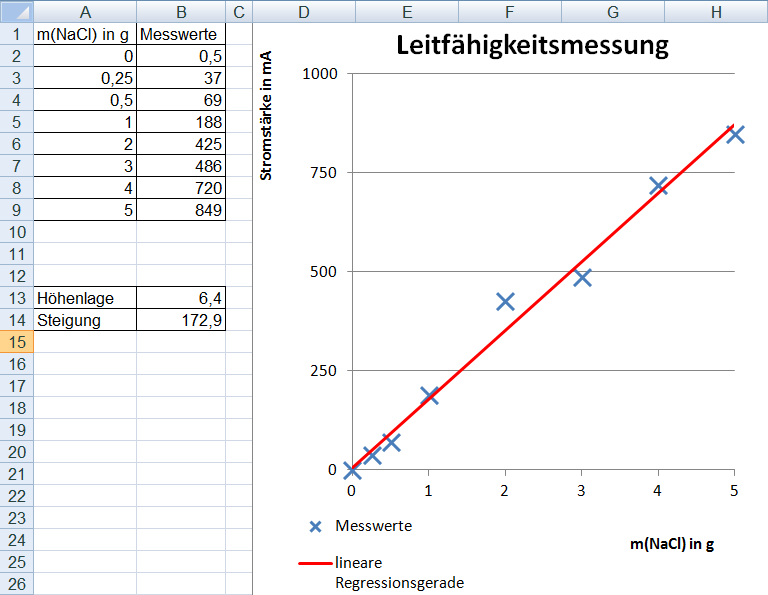
Alle Messwerte werden zunächst tabellarisch zusammengestellt. Als Diagramm ergibt sich hieraus eine Punktwolke. Ziel der Regression ist es, eine Ausgleichsgerade durch die Punktwolke zu legen, deren Abstand zu den in der Praxis aufgenommenen Messwerten möglichst klein ist.
In der Waagerechten (X-Achse) wird üblicherweise die Leitgröße aufgetragen, in unserem Fall die Salzmenge in Gramm. Die von der Leitgröße abhängige Größe wird in der Senkrechten (Y-Achse) aufgetragen, hier die Stromstärke in mA.
Regressionsgerade in Excel berechnen lassen
Mit Excel als "Rechenknecht" kann die Regressionsgerade bequem erstellt werden:
- Erstelle eine Messwerttabelle (Bild).
- Markiere die Datenpunkte, Rechtsklick, "Trendlinie hinzufügen" und "linear" auswählen, Regressionsgerade wird eingezeichnet.
- Steigung m der Regressionsgerade liefert Excel über die Formel STEIGUNG().
- Höhenlage b der Regressionsgeraden liefert Excel über die Formel ACHSENABSCHNITT().
- Setzt man diese Werte unter Berücksichtigung der Einheiten in die allgemeine Geradengleichung y = m · x + b ein, ergibt sich der gesuchte quantitative Zusammenhang zwischen Salzmenge und Stromstärke:
I = 179,9 mA · m(NaCl)/g + 6,4 mA bzw. m(NaCl) = (I - 6,4 mA) · g / 179,9 mA
Nutzen
Hat man sich einmal die Mühe gemacht, Messwerte experimentell zu bestimmen und hierzu eine Regressionsgerade ermittelt, können durch Ablesen an der Regressionsgeraden oder durch Einsetzen in die Funktionsgleichung zur Regressionsgeraden beliebige weitere Werte ermittelt werden, ohne dass erneut gemessen werden muss, z. B.:
- Die Untersuchung einer Meerwasserprobe gemäß Versuchsaufbau ergab einen Messwert von 850 mA.
Wie hoch ist der Salzgehalt der Probe (in g/L)?
Lösung