Dimensionierung von Schraubenverbindungen: Unterschied zwischen den Versionen
(→Hersteller und Händler) |
Dg (Diskussion | Beiträge) |
||
| (87 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Dieser Artikel wurde von [[Benutzer:E_Abali|E Abali]] bearbeitet | Dieser Artikel wurde von [[Benutzer:E_Abali|E Abali]] bearbeitet | ||
| − | + | ||
| + | |||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td width=" | + | <td width="370">__TOC__</td> |
<td> | <td> | ||
| − | + | [[Bild:tornillo.png|717px|]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Warum werden Schraubenverbindungen dimensioniert?== | ==Warum werden Schraubenverbindungen dimensioniert?== | ||
| − | [[Schraubenverbindungen]] werden dimensioniert, weil ein Bruch der Schraube schwerwiegende Folgen haben kann (z. | + | [[Schraubenverbindungen]] werden [[Dimensionierung|dimensioniert]], weil ein Bruch der [[Schraubenverbindungen|Schraube]] schwerwiegende Folgen haben kann (z. B. [[Maschinen und Geräte| Kraftmaschinen]]) wenn die [[Fügen| Verbindung]] dicht sein muss (z. B. Druckbehältern) und wenn die [[Fügen| Verbindung]] nicht rutschen darf (z. B. [[Kupplungen]]). Wenn eine gefühlsmäßige Auslegung zu unsicher ist, muss [[Dimensionierung|dimensioniert]] werden. |
==Vorauslegung der Schraubenverbindung== | ==Vorauslegung der Schraubenverbindung== | ||
| − | + | Für den Schraubendurchmesser und die [[Festigkeitsklasse]], die für die [[Dimensionierung|Auslegung]] der [[Schraubenverbindungen]] erforderlich sind, werden mit Hilfe einer Tabelle Richtwerte vorgewählt. Es muss beachtet werden, dass die axial bzw. quer wirkende [[Dimensionierung von Schraubenverbindungen#Statische Betriebskraft als Längskraft|Betriebskraft]] ''F<sub>B</sub>'' auf den nächst höheren Tabellenwert aufgerundet wird. | |
| − | Für den Schraubendurchmesser und die Festigkeitsklasse, die für die Auslegung der Schraubenverbindungen erforderlich sind, | + | |
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
=Berechnung der Schraubenverbindung= | =Berechnung der Schraubenverbindung= | ||
| − | Die Berechnung teilt sich in vorgespannte und nicht vorgespannte Verbindungen. Im Maschinenbau kommen häufiger vorgespannte Verbindungen in Einsatz. | + | Die Berechnung teilt sich in vorgespannte und nicht vorgespannte [[Fügen |Verbindungen]]. Im Maschinenbau kommen häufiger vorgespannte Verbindungen in Einsatz. |
| − | Bei nicht vorgespannten Schraubenverbindungen sind die Schrauben | + | * Bei nicht vorgespannten [[Schraubenverbindungen]] sind die Schrauben nicht festgedreht, also unbelastet vor dem Angreifen einer äußeren Kraft z. B. Spannschlösser. |
| − | nicht festgedreht also unbelastet vor dem Angreifen einer äußeren Kraft z.B Spannschlösser. | + | * Bei vorgespannten [[Fügen|Verbindungen]] sind die Schrauben festgedreht (z. B. mit einer Mutter), also mit einer [[Dimensionierung von Schraubenverbindungen#Vorspannkraft | Vorspannkraft]] ''F<sub>V</sub>'' bereits vor dem Angreifen der [[Dimensionierung von Schraubenverbindungen#Statische Betriebskraft als Längskraft | Betriebskraft]] ''F<sub>B</sub>'' belastet. |
| − | Bei vorgespannten Verbindungen sind die Schrauben festgedreht (z. | ||
| − | |||
== Kraft- und Verformungsverhältnisse == | == Kraft- und Verformungsverhältnisse == | ||
| − | + | Kräfte und Verformungen werden bei Schrauben und verspannten Teilen untersucht, um rechnerisch eine sichere [[Schraubenverbindung]] auslegen zu können, um somit schwerwiegende Folgen (z. B. Brüche) zu vermeiden. | |
| − | Kräfte und Verformungen werden bei Schrauben und verspannten Teilen untersucht um rechnerisch eine sichere Schraubenverbindung auslegen zu können, um somit schwerwiegende Folgen (z.B. Brüche) zu vermeiden. | ||
'''a) eine nicht vorgespannte Verbindung''' | '''a) eine nicht vorgespannte Verbindung''' | ||
| − | <br />'''b) vorgespannte | + | <br />'''b) vorgespannte Verbindung vor dem Festdrehen''' |
<br />(Schraube und Bauteil unbelastet!) | <br />(Schraube und Bauteil unbelastet!) | ||
<br />'''c) nach dem Festdrehen''' | <br />'''c) nach dem Festdrehen''' | ||
<br />(der sog. Montagezustand hier ist die Schraube belastet durch F<sub> V</sub>) | <br />(der sog. Montagezustand hier ist die Schraube belastet durch F<sub> V</sub>) | ||
| − | <br />'''d) nach dem Angreifen der | + | <br />'''d) nach dem Angreifen der [[Dimensionierung von Schraubenverbindungen#Statische Betriebskraft als Längskraft | Betriebskraft]] ''' |
| − | <br />(der sog. | + | <br />(der sog. Betriebszustand) |
===Vorspannkraft=== | ===Vorspannkraft=== | ||
| − | Mit dem | + | Mit dem Festdrehen der Schraube werden die Bauteile um ''f<sub>T</sub>'' zusammen gedrückt und die Schraube um ''f<sub>S</sub>'' verlängert. Durch die Verlängerung (Streckung) der Schraube entsteht die Vorspannkraft ''F<sub>V</sub>''. Die Klemmkraft ''F<sub>Kl</sub>'' der Teile entsteht durch das Zusammendrücken der Teile. Im Montagezustand gilt ''F<sub>V</sub> = F<sub>Kl</sub>''. |
'''Das Verhältnis von Längenänderung und Kraft ist die elastische | '''Das Verhältnis von Längenänderung und Kraft ist die elastische | ||
| Zeile 46: | Zeile 42: | ||
===Nachgiebigkeit der Schraube=== | ===Nachgiebigkeit der Schraube=== | ||
| − | Eine Schraube setzt sich aus mehreren Elementen zusammen. Durch Summieren aller Nachgiebigkeiten der einzelnen Elemente erhält man die | + | Eine Schraube setzt sich aus mehreren Elementen zusammen. Durch Summieren aller Nachgiebigkeiten der einzelnen Elemente erhält man die Nachgiebigkeit der gesamten Schraube. |
| − | |||
===Nachgiebigkeit der verspannten Teile=== | ===Nachgiebigkeit der verspannten Teile=== | ||
| − | Bei den verspannten Teilen muss der Verformungsbereich ermittelt werden, dieser verbreitet sich zur Trennfuge hin. Der Verformungsbereich wird durch einen Ersatzzylinder | + | Bei den verspannten Teilen muss der Verformungsbereich ermittelt werden, dieser verbreitet sich zur Trennfuge hin. Der Verformungsbereich wird durch einen Ersatzzylinder ersetzt um ihn ermitteln zu können. |
| + | ===Statische Betriebskraft als Längskraft=== | ||
| + | Eine statische Betriebskraft ist konstant. Wird die Schraube durch die Betriebskraft auf Zug beansprucht, verlängert sie sich zusätzlich um ''Δf<sub>S</sub>'' und die verspannten Teile werden um den gleichen Betrag ''Δf<sub>T</sub>'' entspannt. Dadurch vermindert sich die [[Dimensionierung von Schraubenverbindungen#Vorspannkraft | Vorspannkraft]] ''F<sub>V</sub>'' auf eine (Rest-) Klemmkraft ''F<sub>KL</sub> = F<sub>V</sub> - F<sub>BT</sub>'', das ist der sog. Vorspannkraftverlust. Bei einer Druckkraft nimmt die Belastung der Schraube ab und die verspannten Teile werden zusätzlich gedrückt, somit wird die Klemmkraft größer ''F<sub>KL</sub> = F<sub>V</sub> + F<sub>BT</sub>''. | ||
| − | |||
| − | |||
| − | |||
| − | |||
[[Bild:Schrauben(3).png|758px|]] | [[Bild:Schrauben(3).png|758px|]] | ||
| − | |||
| − | + | Zum Bild: | |
| − | + | a) Vorspannungs- (Montage-)zustand b) Betriebszustand c) Verspannungsschaubild | |
| − | |||
| − | + | ====Verspannungsschaubild==== | |
| − | + | Ein Verspannungsschaubild dient zur bildlichen Darstellung der Kraft- und Längenverhältnisse bei Schraubenverbindungen. Bei einem Verspannungsschaubild ist die Längenänderung f auf der X-Achse der Kraft auf der Y-Achse gegenüber gestellt. | |
| − | |||
| − | + | === Dynamische Betriebskraft als Längskraft=== | |
| + | Die dynamische Betriebskraft verändert sich zwischen einem oberen Grenzwert ''F<sub>BO</sub>'' und einem unteren Grenzwert ''F<sub>BU</sub>''. Dadurch wird die Schraube schwankend belastet. Um sich das vorstellen zu können, wird sich eine ruhende Mittelkraft ''F<sub>m</sub>'' gedacht um diese pendelt die Ausschlagkraft ''F<sub>a</sub>''. Die Ausschlagkraft ''F<sub>a</sub>'' ist von großer Bedeutung für die Dauerhaltbarkeit der Schraube. | ||
| + | Das Verspannungsschaubild c. zeigt die Verhältnisse bei einer wechselnden Zug-Druckbeanspruchung. | ||
===Einfluss der Krafteinleitung in die Verbindung=== | ===Einfluss der Krafteinleitung in die Verbindung=== | ||
| − | Bei Vereinfachungen wird meist angenommen dass die Betriebskraft F<sub>B</sub> durch die äußeren Ebenen eingeleitet wird. Im Normalfall ist das nicht so. Sondern irgendwo innerhalb der verspannten Teile wird sie in die Verbindung eingeleitet. Somit wird nur ein Teil des Verspannungsbereiches entlastet. Der Entlastete Bereich ist n*lk. | + | Bei Vereinfachungen wird meist angenommen, dass die [[Dimensionierung von Schraubenverbindungen#Statische Betriebskraft als Längskraft | Betriebskraft]] ''F<sub>B</sub>'' durch die äußeren Ebenen eingeleitet wird. Im Normalfall ist das nicht so. Sondern irgendwo innerhalb der verspannten Teile wird sie in die [[Fügen | Verbindung]] eingeleitet. Somit wird nur ein Teil des Verspannungsbereiches entlastet. Der Entlastete Bereich ist ''n*lk''. |
| − | Der durch F<sub>B</sub> entlastete Bereich ist kaum exakt zu berechnen | + | Der durch die [[Dimensionierung von Schraubenverbindungen#Statische Betriebskraft als Längskraft|Betriebskraft]] ''F<sub>B</sub>'' entlastete Bereich ist kaum exakt zu berechnen. Deshalb wird mit einem Kraft Einleitungsfaktor ''n'' gerechnet. |
| − | Die Betriebskraft sollte möglichst nah an der Trennfuge eingeleitet werden. Dadurch kann die Dauerhaltbarkeit der Schraubenverbindung erhöht werden. | + | Die [[Dimensionierung von Schraubenverbindungen#Statische Betriebskraft als Längskraft|Betriebskraft]] sollte möglichst nah an der Trennfuge eingeleitet werden. Dadurch kann die Dauerhaltbarkeit der Schraubenverbindung erhöht werden. |
===Kraftverhältnisse bei statischer oder dynamischer Querkraft=== | ===Kraftverhältnisse bei statischer oder dynamischer Querkraft=== | ||
| − | Von einer Querkraft F<sub>Q</sub> ist dann die Rede, wenn die Betriebskraft (Wirkkraft) senkrecht zur Schraubenachse wirkt. | + | Von einer Querkraft ''F<sub>Q</sub>'' ist dann die Rede, wenn die [[Dimensionierung von Schraubenverbindungen#Statische Betriebskraft als Längskraft | Betriebskraft]] (Wirkkraft) senkrecht zur Schraubenachse wirkt. |
| − | Bei einer | + | Bei einer querbelasteten [[Schraubenverbindung]] sollen die Schrauben ein Verschieben der Teile verhindern. Dafür muss die Querkraft ''F<sub>Q</sub>'' von einer Reibungskraft F<sub>R</sub> aufgenommen werden. |
| − | Die Reibungskraft F<sub>R</sub> entsteht durch eine entsprechend hohe Vorspannkraft der Schrauben, zwischen den Berührungsflächen der verspannten Teile. | + | |
| − | Die Reibungskraft muss F<sub>R</sub> > F<sub>Q</sub> sein, damit die Schrauben dann nur noch statisch auf Zug beansprucht werden. | + | Die Reibungskraft ''F<sub>R</sub>'' entsteht durch eine entsprechend hohe [[Dimensionierung von Schraubenverbindungen#Vorspannkraft | Vorspannkraft]] der Schrauben, zwischen den Berührungsflächen der verspannten Teile. |
| + | Die Reibungskraft muss ''F<sub>R</sub> > F<sub>Q</sub>'' sein, damit die Schrauben dann nur noch statisch auf Zug beansprucht werden. | ||
=== Setzverhalten === | === Setzverhalten === | ||
| − | Zur Montage einer Schraubenverbindung wird eine Montageverspannkraft F<sub>VM</sub> über den Schraubenkopf (bzw. die Mutter) in die Verbindung eingeleitet. | + | Zur Montage einer [[Schraubenverbindung]] wird eine [[Dimensionierung von Schraubenverbindungen#Montagevorspannkraft, Anziehfaktor und Anziehverfahren | Montageverspannkraft]] F<sub>VM</sub> über den Schraubenkopf (bzw. die Mutter) in die Verbindung eingeleitet. |
| − | Bereits während der Montage gleichen sich die Berührungsflächen einander an. Nach der Montage kommt es zu einer plastischen Verformung der zusammengepressten Verschraubungselemente. Hierbei spricht man von einem Setzen der Schraubenverbindung. Dieses Setzen der Verbindung führt zu einem Vorspannkraftverlust F<sub>Z</sub>. | + | |
| − | Ist der Vorspannkraftverlust F<sub>Z</sub> so groß das die (Rest-) Klemmkraft = 0 ist, würden die Teile lose aufeinander liegen, d.h. die Verbindung wäre locker. | + | Bereits während der Montage gleichen sich die Berührungsflächen einander an. Nach der Montage kommt es zu einer plastischen Verformung der zusammengepressten Verschraubungselemente. Hierbei spricht man von einem Setzen der Schraubenverbindung. Dieses Setzen der Verbindung führt zu einem Vorspannkraftverlust F<sub>Z</sub>. |
| − | Deshalb muss eine entsprechend hohe Montageverspannkraft F<sub>VM</sub> gewählt werden um eine geforderte Klemmkraft zu gewährleisten. | + | |
| + | Ist der Vorspannkraftverlust F<sub>Z</sub> so groß das die (Rest-) Klemmkraft = 0 ist, würden die Teile lose aufeinander liegen, d. h. die [[Fügen | Verbindung]] wäre locker. | ||
| + | |||
| + | Deshalb muss eine entsprechend hohe Montageverspannkraft F<sub>VM</sub> gewählt werden um eine geforderte Klemmkraft zu gewährleisten. Vorspannkraftverluste können durch [[Sicherungselemente#Setzsicherungen | Setzsicherungen ]] verhindert werden. | ||
==Berechnung der Sicherheit== | ==Berechnung der Sicherheit== | ||
=== Dauerhaltbarkeit, dynamische Sicherheit === | === Dauerhaltbarkeit, dynamische Sicherheit === | ||
Im Maschinenbau treten meistens dynamische Belastungen auf. Die Schraube wird durch die Betriebskraft schwingend belastet. Dadurch wird ihre Haltbarkeit deutlich herabgesetzt. Die durch die dynamische Belastung gegebenen Ausschlagskraft F<sub>a</sub> führt zu einer Ausschlagspannung σ<sub>a</sub>. Durch die Ausschlagspannung σ<sub>a</sub> und eine gegebene Ausschlagfestigkeit σ<sub>A</sub> kann die dynamische Sicherheit einer Schraube überprüft werden. Das Verhältnis zwischen Ausschlagfestigkeit und Ausschlagspannung ist gleich die dynamische Sicherheit, | Im Maschinenbau treten meistens dynamische Belastungen auf. Die Schraube wird durch die Betriebskraft schwingend belastet. Dadurch wird ihre Haltbarkeit deutlich herabgesetzt. Die durch die dynamische Belastung gegebenen Ausschlagskraft F<sub>a</sub> führt zu einer Ausschlagspannung σ<sub>a</sub>. Durch die Ausschlagspannung σ<sub>a</sub> und eine gegebene Ausschlagfestigkeit σ<sub>A</sub> kann die dynamische Sicherheit einer Schraube überprüft werden. Das Verhältnis zwischen Ausschlagfestigkeit und Ausschlagspannung ist gleich die dynamische Sicherheit, | ||
| − | S<sub>D</sub> = σ<sub>A</sub> / σ<sub>a</sub>. Die errechnete Sicherheit wird mit der erforderlichen Sicherheit verglichen und darf nicht kleiner als diese sein, somit gilt S<sub>D</sub> ≥ S<sub>Derf</sub>.Die erforderliche Sicherheit beträgt 1,2. | + | S<sub>D</sub> = σ<sub>A</sub> / σ<sub>a</sub>. Die errechnete Sicherheit wird mit der erforderlichen Sicherheit verglichen und darf nicht kleiner als diese sein, somit gilt S<sub>D</sub> ≥ S<sub>Derf</sub>. Die erforderliche Sicherheit beträgt 1,2. |
| − | |||
=== Statische Sicherheit, Einhaltung der maximalen zulässigen Schraubenkraft === | === Statische Sicherheit, Einhaltung der maximalen zulässigen Schraubenkraft === | ||
| − | Die Mindestdehngrenze der Schraube wird im vorgespannten zustand zu 90% ausgenutzt (σ<sub>red</sub> = 0,9 ∙ R<sub>p0,2</sub>), das heißt die Betriebskraft F<sub>B</sub> darf die Schraube nicht über 10% zusätzlich belasten, also gilt für die Zusatzkraft | + | Die Mindestdehngrenze der Schraube wird im vorgespannten zustand zu 90% ausgenutzt (σ<sub>red</sub> = 0,9 ∙ R<sub>p0,2</sub>), das heißt die [[Dimensionierung von Schraubenverbindungen#Statische Betriebskraft als Längskraft | Betriebskraft]] F<sub>B</sub> darf die Schraube nicht über 10% zusätzlich belasten, also gilt für die Zusatzkraft |
F<sub>BS</sub> < 0,1 – R<sub>p0,2</sub> ∙ A<sub>S</sub>. | F<sub>BS</sub> < 0,1 – R<sub>p0,2</sub> ∙ A<sub>S</sub>. | ||
| − | Die statische Sicherheit S<sub>F</sub> ist das Verhältnis von der 0,2%-Streckgrenze R<sub>p0,2</sub> zur Vergleichsspannung σred, daraus ergibt sich S<sub>F</sub> = R<sub>p0,2</sub> / | + | Die statische Sicherheit S<sub>F</sub> ist das Verhältnis von der 0,2%-Streckgrenze R<sub>p0,2</sub> zur Vergleichsspannung σred, daraus ergibt sich S<sub>F</sub> = R<sub>p0,2</sub> / σ<sub>red</sub>. Die errechnete Sicherheit wird mit der erforderlichen Sicherheit verglichen und darf nicht kleiner als diese sein, somit gilt S<sub>F</sub> ≥ S<sub>Ferf</sub>. |
=== Flächenpressung === | === Flächenpressung === | ||
Damit auch bei maximaler Schraubenkraft an der Auflagefläche zwischen Schraubenkopf bzw. Mutter und den verspannten Teilen keine weiteren Setzerscheinungen ausgelöst werden, darf die Flächenpressung die Quetschgrenze des verspannten Werstoffen nicht überschreiten. Die Flächenpressung wird errechnet und mit der Quetschgrenze der verspannten Teile verglichen. | Damit auch bei maximaler Schraubenkraft an der Auflagefläche zwischen Schraubenkopf bzw. Mutter und den verspannten Teilen keine weiteren Setzerscheinungen ausgelöst werden, darf die Flächenpressung die Quetschgrenze des verspannten Werstoffen nicht überschreiten. Die Flächenpressung wird errechnet und mit der Quetschgrenze der verspannten Teile verglichen. | ||
| − | |||
| − | |||
| − | |||
| Zeile 118: | Zeile 110: | ||
===Kräfte am Gewinde (Vereinfacht)=== | ===Kräfte am Gewinde (Vereinfacht)=== | ||
| − | Das Bild zeigt vereinfacht dargestellt Kraftverhältnisse an jeweils einem Gewindegang. Der Steigungswinkel der schiefen Ebene ist gleich der Gewindesteigungswinkel φ. Das Muttergewinde wurde durch den Gleitkörper ersetzt, an dem die Längskraft F, die Umfangskraft | + | Das Bild zeigt vereinfacht dargestellt Kraftverhältnisse an jeweils einem Gewindegang. Der Steigungswinkel der schiefen Ebene ist gleich der Gewindesteigungswinkel φ. Das Muttergewinde wurde durch den Gleitkörper ersetzt, an dem die Längskraft F, die Umfangskraft F<sub>u</sub>und Die Ersatzkraft Fe angreifen. Das dargestellte Krafteck muss bei Gleichgewicht geschlossen sein. |
| − | Die Umfangskraft F<sub>u</sub> wird benötigt um | + | Die Umfangskraft ''F<sub>u</sub>'' wird benötigt, um das Gewindemoment zu errechnen. ''M<sub>G</sub> = F<sub>u</sub> ∙ d<sub>2</sub> / 2 |
| − | + | '' | |
| − | |||
| − | + | b) „Last heben“ entspricht dem Festdrehen der Schraube, hier ergibt sich aus dem Krafteck, ''F<sub>u</sub> = F ∙ tan (φ + ρ) | |
| − | b) „Last heben“ entspricht dem Festdrehen der Schraube, hier ergibt sich aus dem Krafteck, F<sub>u</sub> = F ∙ tan (φ + ρ) | + | '' |
| − | + | c) „Last senken“ entspricht dem Lösen der Schraube, hier ergibt sich aus dem Krafteck, ''F<sub>u</sub> = F ∙ tan (φ - ρ)'' | |
| − | c) „Last senken“ entspricht dem Lösen der Schraube, hier ergibt sich aus dem Krafteck, F<sub>u</sub> = F ∙ tan (φ - ρ) | ||
d) hier ist Steigungswinkel φ < Reibungswinkel ρ, (φ - ρ) wird negativ und damit auch F<sub>u</sub> d.h. es muss zusätzlich Fu zum Lösen aufgebracht werden, das entspricht dem Lösen einer Schraube mit selbsthemmendem Gewinde | d) hier ist Steigungswinkel φ < Reibungswinkel ρ, (φ - ρ) wird negativ und damit auch F<sub>u</sub> d.h. es muss zusätzlich Fu zum Lösen aufgebracht werden, das entspricht dem Lösen einer Schraube mit selbsthemmendem Gewinde | ||
| − | === | + | ===Anziehdrehmoment M<sub>A</sub>=== |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Um eine [[Schraubenverbindung ]] festzudrehen wird ein bestimmter Kraftaufwand benötigt. Beim Festdrehen der Schraube entsteht Reibung zwischen den Berührungsflächen. Deshalb muss beim Anziehen neben des Gewindemomentes M<sub>G</sub> auch das Reibungsmoment M<sub>RA</sub> überwunden werden. Daraus ergibt sich das Anziehdrehmoment M<sub>A</sub> = M<sub>G</sub> + M<sub>RA</sub> | |
| − | |||
| − | |||
| − | + | Es gibt eine vereinfachte Formel für das Anziehdrehmoment, bei der das aufwendig zu berechnende Gewindemoment und Reibungsmoment nicht benötigt werden. Der Klammerausdruck der oben aufgeführten Formel wird ersetzt durch K ∙ d. Daraus ergibt sich für das Anziehdrehmoment '''M<sub>A</sub> = F<sub>VM</sub> ∙ K ∙ d'''. Die K-Werte liegen für die üblichen Reibungszahlen μ<sub>G</sub> und μ<sub>K</sub> von 0,08 bis 0,14 entsprechend zwischen 0,12 und 0,19. | |
| − | |||
| − | + | === Montagevorspannkraft, Anziehfaktor und Anziehverfahren === | |
| − | + | Die [[Dimensionierung von Schraubenverbindungen#Vorspannkraft | Vorspannkraft]] unterliegt bei der Montage einer Streuung zwischen einem Größtwert ''F<sub>Vmax</sub>'' und einem Kleinstwert ''F<sub>Vmin</sub>'', das muss bei der Auslegung einer Schraubenverbindung berücksichtigt werden. | |
| − | + | Das Anziehen ohne Einstellkontrollen (z. B. von Hand) führt zu den größten Streuungen. Bei wichtigen Verschraubungen ist ein kontrolliertes Anziehen unbedingt erforderlich, um möglichst genau eine geforderte Vorspannkraft zu erreichen. Für das kontrollierte Anziehen der Verbindung gibt es verschiedene Schraubenanziehgeräte. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''a)''' Signalgebender Drehmomentschlüssel mit Schnellverstellung | '''a)''' Signalgebender Drehmomentschlüssel mit Schnellverstellung | ||
| − | Beim Drehmoment gesteuertem Anziehen mit anzeigenden oder signalgebenden | + | Beim Drehmoment gesteuertem Anziehen mit anzeigenden oder signalgebenden Drehmomentschlüssel, auftretende Streuung der Montagevorspannkraft, wird im Wesentlichen durch die Steuerung des Anziehdrehmoments und der Reibungen hervorgerufen. |
| − | '''b)''' Elektronischer Messschlüssel für | + | '''b)''' Elektronischer Messschlüssel für drehmoment-, drehwinkel- und streckgrenzengesteuertes Anziehen |
| − | |||
| − | Beim | + | Beim drehwinkelgesteuerten Anziehen wird die Schraube auf ein Ausgangsdrehmoment vorgezogen, wodurch die Bauteile zur Anlage kommen. Von dieser Drehmomentschwelle aus wird die Schraube um einen errechneten Winkel weiter bewegt und in den überelastischen Bereich vorgepresst. |
| − | |||
| − | + | Beim streckgrenzengesteuerten Anziehen, wird das Verhältnis von Anziehdrehmoment zu Anziehwinkel stetig gemessen, beim Erreichen der Schraubenstreckgrenze wird der Anziehvorgang beendet. | |
| + | Beim drehwinkel- und streckgrenzgesteuerten Anziehen beeinflussen Schraubenstreckgrenze und Gewindereibung die Streuung. | ||
| + | '''c)''' Kraftvielfältiger zum drehmoment- und drehwinkelgesteuerten Anziehen (bis 4.300Nm) großer Schraubenverbindungen, 1 Antrieb, 2 Abtriebsvierkant, 3 Planetengetriebe (i=4...20), 4 Abstützarm | ||
| + | ====Anziehfaktor==== | ||
| + | Das Maß für die Streuung der [[Dimensionierung von Schraubenverbindungen#Vorspannkraft | Vorspannkraft]] ist der Anziehfaktor k<sub>A</sub>. Dieser ergibt sich aus dem Verhältnis zwischen F<sub>Vmax</sub> und F<sub>Vmin</sub>, somit gilt '''k<sub>A</sub> = F<sub>Vmax</sub> / F<sub>Vmin</sub> > 1'''. | ||
| + | Damit die Einhaltung der Mindestvorspannkraft im Betriebszustand mit Sicherheit gewährleistet ist, muss mit der maximalen [[Dimensionierung von Schraubenverbindungen#Vorspannkraft | Vorspannkraft]] gerechnet werden. | ||
| + | === Lösen einer Schraubenverbindung, Losdrehmoment:=== | ||
| + | Das zum Lösen einer vorgespannten Schraubenverbindung erforderliche Losdrehmoment ist normalerweise kleiner als das Anziehdrehmoment, da sich einmal Montagevorspannskraft F<sub>VM</sub> wegen des Setzens auf eine vorhandene Vorspannkraft verringert hat und zum anderen die Mechanischen Zusammenhänge ein Lösen begünstigen. | ||
| − | == | + | =Übungsaufgaben= |
| − | |||
| − | |||
| − | == | + | ==Übungsaufgabe 1== |
| − | + | Ein Blindflansch soll mit 6 Sechskantschrauben der Festigkeitsklasse 10.9 abgedichtet werden. Die aufzunehmende Gesamtkraft beträgt F<sub>ges</sub> = 300 kN, die Sicherheit 1,5. Welche Schraubengröße muss verwendet werden? [[Dimensionierung von Schraubenverbindungen: Lösung|Lösung]] | |
| + | ==Übungsaufgabe 2== | ||
| − | + | Für die Verschraubung des Deckels eines Druckbehälters sind Festigkeitsklasse und Anzahl der im Entwurf festgelegten Sechskantschrauben M20 ''überschlägig'' zu ermitteln. Es wird ein Welldichtring (''d<sub> a</sub>'' = 650 mm, d<sub> i</sub> = 610 mm) eingelegt. Der Lochkreisdurchmesser ist auf D = 700 mm festgelegt. Der Behälter hat einen Innendurchmesser von d<sub> i</sub> = 600 mm und steht unter dem konstanten inneren Gasdruck p<sub> e</sub> = 8 bar. | |
| − | |||
[[Bild:Schrauben(9).jpg| 222px| center|Druckbehälter]] | [[Bild:Schrauben(9).jpg| 222px| center|Druckbehälter]] | ||
| Zeile 196: | Zeile 170: | ||
[[Dimensionierung von Schraubenverbindungen: Lösung|Lösung]] | [[Dimensionierung von Schraubenverbindungen: Lösung|Lösung]] | ||
| − | + | =Wiederholungsfragen= | |
# Wie entsteht die Vorspannkraft? [[Dimensionierung von Schraubenverbindungen: Antworten| Antwort]] | # Wie entsteht die Vorspannkraft? [[Dimensionierung von Schraubenverbindungen: Antworten| Antwort]] | ||
| − | |||
# Was ist die Nachgiebigkeit? [[Dimensionierung von Schraubenverbindungen: Antworten| Antwort]] | # Was ist die Nachgiebigkeit? [[Dimensionierung von Schraubenverbindungen: Antworten| Antwort]] | ||
| − | |||
# Was ist der Unterschied zwischen einer statischen Betriebskraft und einer dynamischen Betriebskraft? [[Dimensionierung von Schraubenverbindungen: Antworten| Antwort]] | # Was ist der Unterschied zwischen einer statischen Betriebskraft und einer dynamischen Betriebskraft? [[Dimensionierung von Schraubenverbindungen: Antworten| Antwort]] | ||
| − | |||
# Was ist unterdem Setzen eine Schraubenverbindung zu verstehen? [[Dimensionierung von Schraubenverbindungen: Antworten| Antwort]] | # Was ist unterdem Setzen eine Schraubenverbindung zu verstehen? [[Dimensionierung von Schraubenverbindungen: Antworten| Antwort]] | ||
| − | |||
# Warum ist bei wichtigen Verschraubungen ein kontrolliertes Anziehen unbedingt notwendig? [[Dimensionierung von Schraubenverbindungen: Antworten| Antwort]] | # Warum ist bei wichtigen Verschraubungen ein kontrolliertes Anziehen unbedingt notwendig? [[Dimensionierung von Schraubenverbindungen: Antworten| Antwort]] | ||
| − | + | =Hersteller und Händler= | |
| − | + | '''Lieferanten:''' | |
| + | [http://www.wuerth.de/| Wuerth]; [http://online-schraubenhandel.de/| Online-Schraubenhandel] | ||
Eine Schraubenhersteller Zuordnung Nach Produkten [http://www.schraubenverband.de/webd002d.htm| Welche schraube brauchen Sie?] | Eine Schraubenhersteller Zuordnung Nach Produkten [http://www.schraubenverband.de/webd002d.htm| Welche schraube brauchen Sie?] | ||
| − | == Quellen | + | =Powerpoint-Präsentation= |
| + | Eine Powerpoint-Präsentation zum Runterladen [[Media: Dimensionierung_von_Schraubenverbindungen.ppt]] | ||
| + | |||
| + | = Quellen= | ||
# Roloff/Matek: Maschinenelemente-Tabellenbuch, Vieweg Verlag, 18. Aufl. 2007, ISBN 3-834-80262-X, €36,90. | # Roloff/Matek: Maschinenelemente-Tabellenbuch, Vieweg Verlag, 18. Aufl. 2007, ISBN 3-834-80262-X, €36,90. | ||
# Roloff/Matek: Maschinenelemente-Formelsammlung, Vieweg Verlag, 8. Aufl. 2006. ISBN 3-834-80119-4, €20,90. | # Roloff/Matek: Maschinenelemente-Formelsammlung, Vieweg Verlag, 8. Aufl. 2006. ISBN 3-834-80119-4, €20,90. | ||
# Tabellenbuch Metall, 43. Auflage. Europa Verlag, ISBN 3-8085-1673-9, €21,50 | # Tabellenbuch Metall, 43. Auflage. Europa Verlag, ISBN 3-8085-1673-9, €21,50 | ||
| + | |||
| + | --[[Benutzer:E Abali|E Abali]] 23:40, 11. Okt. 2008 (CEST) | ||
[[Kategorie: Entwicklung und Konstruktion]] | [[Kategorie: Entwicklung und Konstruktion]] | ||
Aktuelle Version vom 28. Februar 2022, 11:53 Uhr
Dieser Artikel wurde von E Abali bearbeitet
Berechnung der Schraubenverbindung
Die Berechnung teilt sich in vorgespannte und nicht vorgespannte Verbindungen. Im Maschinenbau kommen häufiger vorgespannte Verbindungen in Einsatz.
- Bei nicht vorgespannten Schraubenverbindungen sind die Schrauben nicht festgedreht, also unbelastet vor dem Angreifen einer äußeren Kraft z. B. Spannschlösser.
- Bei vorgespannten Verbindungen sind die Schrauben festgedreht (z. B. mit einer Mutter), also mit einer Vorspannkraft FV bereits vor dem Angreifen der Betriebskraft FB belastet.
Kraft- und Verformungsverhältnisse
Kräfte und Verformungen werden bei Schrauben und verspannten Teilen untersucht, um rechnerisch eine sichere Schraubenverbindung auslegen zu können, um somit schwerwiegende Folgen (z. B. Brüche) zu vermeiden.
a) eine nicht vorgespannte Verbindung
b) vorgespannte Verbindung vor dem Festdrehen
(Schraube und Bauteil unbelastet!)
c) nach dem Festdrehen
(der sog. Montagezustand hier ist die Schraube belastet durch F V)
d) nach dem Angreifen der Betriebskraft
(der sog. Betriebszustand)
Vorspannkraft
Mit dem Festdrehen der Schraube werden die Bauteile um fT zusammen gedrückt und die Schraube um fS verlängert. Durch die Verlängerung (Streckung) der Schraube entsteht die Vorspannkraft FV. Die Klemmkraft FKl der Teile entsteht durch das Zusammendrücken der Teile. Im Montagezustand gilt FV = FKl.
Das Verhältnis von Längenänderung und Kraft ist die elastische Nachgiebigkeit δ = f / F
Nachgiebigkeit der Schraube
Eine Schraube setzt sich aus mehreren Elementen zusammen. Durch Summieren aller Nachgiebigkeiten der einzelnen Elemente erhält man die Nachgiebigkeit der gesamten Schraube.
Nachgiebigkeit der verspannten Teile
Bei den verspannten Teilen muss der Verformungsbereich ermittelt werden, dieser verbreitet sich zur Trennfuge hin. Der Verformungsbereich wird durch einen Ersatzzylinder ersetzt um ihn ermitteln zu können.
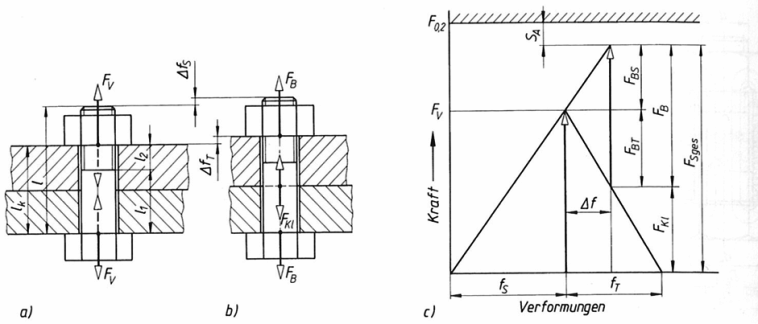
Statische Betriebskraft als Längskraft
Eine statische Betriebskraft ist konstant. Wird die Schraube durch die Betriebskraft auf Zug beansprucht, verlängert sie sich zusätzlich um ΔfS und die verspannten Teile werden um den gleichen Betrag ΔfT entspannt. Dadurch vermindert sich die Vorspannkraft FV auf eine (Rest-) Klemmkraft FKL = FV - FBT, das ist der sog. Vorspannkraftverlust. Bei einer Druckkraft nimmt die Belastung der Schraube ab und die verspannten Teile werden zusätzlich gedrückt, somit wird die Klemmkraft größer FKL = FV + FBT.
Zum Bild:
a) Vorspannungs- (Montage-)zustand b) Betriebszustand c) Verspannungsschaubild
Verspannungsschaubild
Ein Verspannungsschaubild dient zur bildlichen Darstellung der Kraft- und Längenverhältnisse bei Schraubenverbindungen. Bei einem Verspannungsschaubild ist die Längenänderung f auf der X-Achse der Kraft auf der Y-Achse gegenüber gestellt.
Dynamische Betriebskraft als Längskraft
Die dynamische Betriebskraft verändert sich zwischen einem oberen Grenzwert FBO und einem unteren Grenzwert FBU. Dadurch wird die Schraube schwankend belastet. Um sich das vorstellen zu können, wird sich eine ruhende Mittelkraft Fm gedacht um diese pendelt die Ausschlagkraft Fa. Die Ausschlagkraft Fa ist von großer Bedeutung für die Dauerhaltbarkeit der Schraube. Das Verspannungsschaubild c. zeigt die Verhältnisse bei einer wechselnden Zug-Druckbeanspruchung.
Einfluss der Krafteinleitung in die Verbindung
Bei Vereinfachungen wird meist angenommen, dass die Betriebskraft FB durch die äußeren Ebenen eingeleitet wird. Im Normalfall ist das nicht so. Sondern irgendwo innerhalb der verspannten Teile wird sie in die Verbindung eingeleitet. Somit wird nur ein Teil des Verspannungsbereiches entlastet. Der Entlastete Bereich ist n*lk.
Der durch die Betriebskraft FB entlastete Bereich ist kaum exakt zu berechnen. Deshalb wird mit einem Kraft Einleitungsfaktor n gerechnet. Die Betriebskraft sollte möglichst nah an der Trennfuge eingeleitet werden. Dadurch kann die Dauerhaltbarkeit der Schraubenverbindung erhöht werden.
Kraftverhältnisse bei statischer oder dynamischer Querkraft
Von einer Querkraft FQ ist dann die Rede, wenn die Betriebskraft (Wirkkraft) senkrecht zur Schraubenachse wirkt. Bei einer querbelasteten Schraubenverbindung sollen die Schrauben ein Verschieben der Teile verhindern. Dafür muss die Querkraft FQ von einer Reibungskraft FR aufgenommen werden.
Die Reibungskraft FR entsteht durch eine entsprechend hohe Vorspannkraft der Schrauben, zwischen den Berührungsflächen der verspannten Teile. Die Reibungskraft muss FR > FQ sein, damit die Schrauben dann nur noch statisch auf Zug beansprucht werden.
Setzverhalten
Zur Montage einer Schraubenverbindung wird eine Montageverspannkraft FVM über den Schraubenkopf (bzw. die Mutter) in die Verbindung eingeleitet.
Bereits während der Montage gleichen sich die Berührungsflächen einander an. Nach der Montage kommt es zu einer plastischen Verformung der zusammengepressten Verschraubungselemente. Hierbei spricht man von einem Setzen der Schraubenverbindung. Dieses Setzen der Verbindung führt zu einem Vorspannkraftverlust FZ.
Ist der Vorspannkraftverlust FZ so groß das die (Rest-) Klemmkraft = 0 ist, würden die Teile lose aufeinander liegen, d. h. die Verbindung wäre locker.
Deshalb muss eine entsprechend hohe Montageverspannkraft FVM gewählt werden um eine geforderte Klemmkraft zu gewährleisten. Vorspannkraftverluste können durch Setzsicherungen verhindert werden.
Berechnung der Sicherheit
Dauerhaltbarkeit, dynamische Sicherheit
Im Maschinenbau treten meistens dynamische Belastungen auf. Die Schraube wird durch die Betriebskraft schwingend belastet. Dadurch wird ihre Haltbarkeit deutlich herabgesetzt. Die durch die dynamische Belastung gegebenen Ausschlagskraft Fa führt zu einer Ausschlagspannung σa. Durch die Ausschlagspannung σa und eine gegebene Ausschlagfestigkeit σA kann die dynamische Sicherheit einer Schraube überprüft werden. Das Verhältnis zwischen Ausschlagfestigkeit und Ausschlagspannung ist gleich die dynamische Sicherheit, SD = σA / σa. Die errechnete Sicherheit wird mit der erforderlichen Sicherheit verglichen und darf nicht kleiner als diese sein, somit gilt SD ≥ SDerf. Die erforderliche Sicherheit beträgt 1,2.
Statische Sicherheit, Einhaltung der maximalen zulässigen Schraubenkraft
Die Mindestdehngrenze der Schraube wird im vorgespannten zustand zu 90% ausgenutzt (σred = 0,9 ∙ Rp0,2), das heißt die Betriebskraft FB darf die Schraube nicht über 10% zusätzlich belasten, also gilt für die Zusatzkraft FBS < 0,1 – Rp0,2 ∙ AS.
Die statische Sicherheit SF ist das Verhältnis von der 0,2%-Streckgrenze Rp0,2 zur Vergleichsspannung σred, daraus ergibt sich SF = Rp0,2 / σred. Die errechnete Sicherheit wird mit der erforderlichen Sicherheit verglichen und darf nicht kleiner als diese sein, somit gilt SF ≥ SFerf.
Flächenpressung
Damit auch bei maximaler Schraubenkraft an der Auflagefläche zwischen Schraubenkopf bzw. Mutter und den verspannten Teilen keine weiteren Setzerscheinungen ausgelöst werden, darf die Flächenpressung die Quetschgrenze des verspannten Werstoffen nicht überschreiten. Die Flächenpressung wird errechnet und mit der Quetschgrenze der verspannten Teile verglichen.
Anziehen der Verbindung, Anziehdrehmoment
Kräfte am Gewinde (Vereinfacht)
Das Bild zeigt vereinfacht dargestellt Kraftverhältnisse an jeweils einem Gewindegang. Der Steigungswinkel der schiefen Ebene ist gleich der Gewindesteigungswinkel φ. Das Muttergewinde wurde durch den Gleitkörper ersetzt, an dem die Längskraft F, die Umfangskraft Fuund Die Ersatzkraft Fe angreifen. Das dargestellte Krafteck muss bei Gleichgewicht geschlossen sein. Die Umfangskraft Fu wird benötigt, um das Gewindemoment zu errechnen. MG = Fu ∙ d2 / 2
b) „Last heben“ entspricht dem Festdrehen der Schraube, hier ergibt sich aus dem Krafteck, Fu = F ∙ tan (φ + ρ) c) „Last senken“ entspricht dem Lösen der Schraube, hier ergibt sich aus dem Krafteck, Fu = F ∙ tan (φ - ρ)
d) hier ist Steigungswinkel φ < Reibungswinkel ρ, (φ - ρ) wird negativ und damit auch Fu d.h. es muss zusätzlich Fu zum Lösen aufgebracht werden, das entspricht dem Lösen einer Schraube mit selbsthemmendem Gewinde
Anziehdrehmoment MA
Um eine Schraubenverbindung festzudrehen wird ein bestimmter Kraftaufwand benötigt. Beim Festdrehen der Schraube entsteht Reibung zwischen den Berührungsflächen. Deshalb muss beim Anziehen neben des Gewindemomentes MG auch das Reibungsmoment MRA überwunden werden. Daraus ergibt sich das Anziehdrehmoment MA = MG + MRA
Es gibt eine vereinfachte Formel für das Anziehdrehmoment, bei der das aufwendig zu berechnende Gewindemoment und Reibungsmoment nicht benötigt werden. Der Klammerausdruck der oben aufgeführten Formel wird ersetzt durch K ∙ d. Daraus ergibt sich für das Anziehdrehmoment MA = FVM ∙ K ∙ d. Die K-Werte liegen für die üblichen Reibungszahlen μG und μK von 0,08 bis 0,14 entsprechend zwischen 0,12 und 0,19.
Montagevorspannkraft, Anziehfaktor und Anziehverfahren
Die Vorspannkraft unterliegt bei der Montage einer Streuung zwischen einem Größtwert FVmax und einem Kleinstwert FVmin, das muss bei der Auslegung einer Schraubenverbindung berücksichtigt werden. Das Anziehen ohne Einstellkontrollen (z. B. von Hand) führt zu den größten Streuungen. Bei wichtigen Verschraubungen ist ein kontrolliertes Anziehen unbedingt erforderlich, um möglichst genau eine geforderte Vorspannkraft zu erreichen. Für das kontrollierte Anziehen der Verbindung gibt es verschiedene Schraubenanziehgeräte.
a) Signalgebender Drehmomentschlüssel mit Schnellverstellung
Beim Drehmoment gesteuertem Anziehen mit anzeigenden oder signalgebenden Drehmomentschlüssel, auftretende Streuung der Montagevorspannkraft, wird im Wesentlichen durch die Steuerung des Anziehdrehmoments und der Reibungen hervorgerufen.
b) Elektronischer Messschlüssel für drehmoment-, drehwinkel- und streckgrenzengesteuertes Anziehen
Beim drehwinkelgesteuerten Anziehen wird die Schraube auf ein Ausgangsdrehmoment vorgezogen, wodurch die Bauteile zur Anlage kommen. Von dieser Drehmomentschwelle aus wird die Schraube um einen errechneten Winkel weiter bewegt und in den überelastischen Bereich vorgepresst.
Beim streckgrenzengesteuerten Anziehen, wird das Verhältnis von Anziehdrehmoment zu Anziehwinkel stetig gemessen, beim Erreichen der Schraubenstreckgrenze wird der Anziehvorgang beendet. Beim drehwinkel- und streckgrenzgesteuerten Anziehen beeinflussen Schraubenstreckgrenze und Gewindereibung die Streuung.
c) Kraftvielfältiger zum drehmoment- und drehwinkelgesteuerten Anziehen (bis 4.300Nm) großer Schraubenverbindungen, 1 Antrieb, 2 Abtriebsvierkant, 3 Planetengetriebe (i=4...20), 4 Abstützarm
Anziehfaktor
Das Maß für die Streuung der Vorspannkraft ist der Anziehfaktor kA. Dieser ergibt sich aus dem Verhältnis zwischen FVmax und FVmin, somit gilt kA = FVmax / FVmin > 1. Damit die Einhaltung der Mindestvorspannkraft im Betriebszustand mit Sicherheit gewährleistet ist, muss mit der maximalen Vorspannkraft gerechnet werden.
Lösen einer Schraubenverbindung, Losdrehmoment:
Das zum Lösen einer vorgespannten Schraubenverbindung erforderliche Losdrehmoment ist normalerweise kleiner als das Anziehdrehmoment, da sich einmal Montagevorspannskraft FVM wegen des Setzens auf eine vorhandene Vorspannkraft verringert hat und zum anderen die Mechanischen Zusammenhänge ein Lösen begünstigen.
Übungsaufgaben
Übungsaufgabe 1
Ein Blindflansch soll mit 6 Sechskantschrauben der Festigkeitsklasse 10.9 abgedichtet werden. Die aufzunehmende Gesamtkraft beträgt Fges = 300 kN, die Sicherheit 1,5. Welche Schraubengröße muss verwendet werden? Lösung
Übungsaufgabe 2
Für die Verschraubung des Deckels eines Druckbehälters sind Festigkeitsklasse und Anzahl der im Entwurf festgelegten Sechskantschrauben M20 überschlägig zu ermitteln. Es wird ein Welldichtring (d a = 650 mm, d i = 610 mm) eingelegt. Der Lochkreisdurchmesser ist auf D = 700 mm festgelegt. Der Behälter hat einen Innendurchmesser von d i = 600 mm und steht unter dem konstanten inneren Gasdruck p e = 8 bar.
Allgemeine Lösungshinweise :
Es handelt sich um eine exzentrisch verspannte und exzentrisch belastete Schraubenverbindung. Bei der Berechnung der auf den Deckel wirkenden Druckkraft wird davon ausgegangen, dass der Druck bis zum mittleren Dichtungsdurchmesser d m wirksam ist.
Konstruktionsregeln für Flanschverbindungen: Das Verhältnis Schraubenabstand zu Lochdurchmesser la / dh ≤ 5.
Wiederholungsfragen
- Wie entsteht die Vorspannkraft? Antwort
- Was ist die Nachgiebigkeit? Antwort
- Was ist der Unterschied zwischen einer statischen Betriebskraft und einer dynamischen Betriebskraft? Antwort
- Was ist unterdem Setzen eine Schraubenverbindung zu verstehen? Antwort
- Warum ist bei wichtigen Verschraubungen ein kontrolliertes Anziehen unbedingt notwendig? Antwort
Hersteller und Händler
Lieferanten: Wuerth; Online-Schraubenhandel
Eine Schraubenhersteller Zuordnung Nach Produkten Welche schraube brauchen Sie?
Powerpoint-Präsentation
Eine Powerpoint-Präsentation zum Runterladen Media: Dimensionierung_von_Schraubenverbindungen.ppt
Quellen
- Roloff/Matek: Maschinenelemente-Tabellenbuch, Vieweg Verlag, 18. Aufl. 2007, ISBN 3-834-80262-X, €36,90.
- Roloff/Matek: Maschinenelemente-Formelsammlung, Vieweg Verlag, 8. Aufl. 2006. ISBN 3-834-80119-4, €20,90.
- Tabellenbuch Metall, 43. Auflage. Europa Verlag, ISBN 3-8085-1673-9, €21,50
--E Abali 23:40, 11. Okt. 2008 (CEST)