Festigkeitsberechnung: Antworten: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
Wovon hängt die Festigkeit von Bauteilen ab? <br /> | Wovon hängt die Festigkeit von Bauteilen ab? <br /> | ||
| − | Die Festigkeit von Bauteilen hängt im wesentlichen vom Werkstoff, von der Temperatur und vom Behandlungszustand eines Bauteils ab.<br><br><br> | + | Die Festigkeit von Bauteilen hängt im wesentlichen von der Belastungsart, vom Werkstoff, von der Temperatur und vom Behandlungszustand eines Bauteils ab.<br><br><br> |
| Zeile 13: | Zeile 13: | ||
<br><br> | <br><br> | ||
| − | + | Konstruiere das Dauerfestigkeitsschaubild nach Smith für den Werkstoff E335, der auf Biegung belastet wird im Maßstab 50 N/mm² = 1 cm.<br> | |
| + | gegebene Werte sind:<br> | ||
| + | σ<sub>bw</sub> = 290 N/mm²<br /> | ||
| + | a) σ<sub>m</sub> = 100 N/mm²<br> | ||
| + | b) σ<sub>m</sub> = 200 N/mm²<br> | ||
| + | c) σ<sub>m</sub> = 470 N/mm²<br> | ||
| + | R<sub>m</sub> = 590 N/mm²; R<sub>e</sub> = 335 N/mm²<br> | ||
| + | gesucht wird die Ober- und die Unterspannung für a), b) und c)<br> | ||
| − | + | Lösung: | |
| − | + | # bei gleichem Maßstab von x- und y-Achse wird auf der x-Achse die Mittelspannung σ<sub>m</sub> eingetragen, auf der y-Achse ±σ<sub>bw</sub>, | |
| − | + | # R<sub>e</sub> parallel zur x-Achse eintragen | |
| − | + | # R<sub>m</sub> parallel zur x-Achse eintragen | |
| − | + | # vom Koordinatenursprung zu R<sub>m</sub> eine 45°-Hilfslinie ziehen (Schnittpunkt mit R<sub>e</sub> ergibt Punkt E) | |
| − | + | # eine 40°-Hilfslinie von +σ<sub>bw</sub> zu R<sub>m</sub> ziehen (Schnittpunkt mit R<sub>e</sub> ergibt Punkt D) | |
| − | b)<br> | + | # Schnittpunkt von 45°-Hilfslinie und R<sub>m</sub> mit -σ<sub>bw</sub> verbinden |
| − | + | # von Punkt D eine Hilfslinie senkrecht nach unten ziehen bis 6 geschnitten wird (ergibt Punkt G) | |
| − | + | # Punkte G und E verbinden | |
| − | + | # Linien nachziehen von +σ<sub>bw</sub> zu Punkt D, zu Punkt E, zu Punkt G, zu -σ<sub>bw</sub>. <br /><br /> | |
| − | + | [[Bild:DFSAufg3.JPG| 600px]] | |
| − | + | ||
| − | c) Da der Wert 470 N/mm² nicht mehr innerhalb der | + | an den blau markierten Punkten auf der roten Kurve, ließt man für a) und b) die folgenden Werte ab:<br> |
| + | a) σ<sub>u</sub>= - 155 N/mm²; σ<sub>o</sub>= 330 N/mm²<br> | ||
| + | |||
| + | b) σ<sub>u</sub>= 20 N/mm²; σ<sub>o</sub>= 335 N/mm²<br> | ||
| + | |||
| + | c) Da der Wert 470 N/mm² nicht mehr innerhalb der Kurve liegt, weist der Werkstoff für diese Belastung keine Dauerfestigkeit auf!<br><br> | ||
| − | |||
| − | |||
zurück zu [[Festigkeitsberechnung]]<br> | zurück zu [[Festigkeitsberechnung]]<br> | ||
[[Kategorie:Entwicklung und Konstruktion]]<br /> | [[Kategorie:Entwicklung und Konstruktion]]<br /> | ||
Aktuelle Version vom 9. Oktober 2008, 15:22 Uhr
Frage 1: Welche Beanspruchungs- oder Belastungsarten sind Dir bekannt?
Zug-/Druckbeanspruchungen, Biege-, Schub- und Torsionsbeanspruchungen.
Frage 2:
Wovon hängt die Festigkeit von Bauteilen ab?
Die Festigkeit von Bauteilen hängt im wesentlichen von der Belastungsart, vom Werkstoff, von der Temperatur und vom Behandlungszustand eines Bauteils ab.
Lösung DFS-Konstruktion nach Smith
Konstruiere das Dauerfestigkeitsschaubild nach Smith für den Werkstoff E335, der auf Biegung belastet wird im Maßstab 50 N/mm² = 1 cm.
gegebene Werte sind:
σbw = 290 N/mm²
a) σm = 100 N/mm²
b) σm = 200 N/mm²
c) σm = 470 N/mm²
Rm = 590 N/mm²; Re = 335 N/mm²
gesucht wird die Ober- und die Unterspannung für a), b) und c)
Lösung:
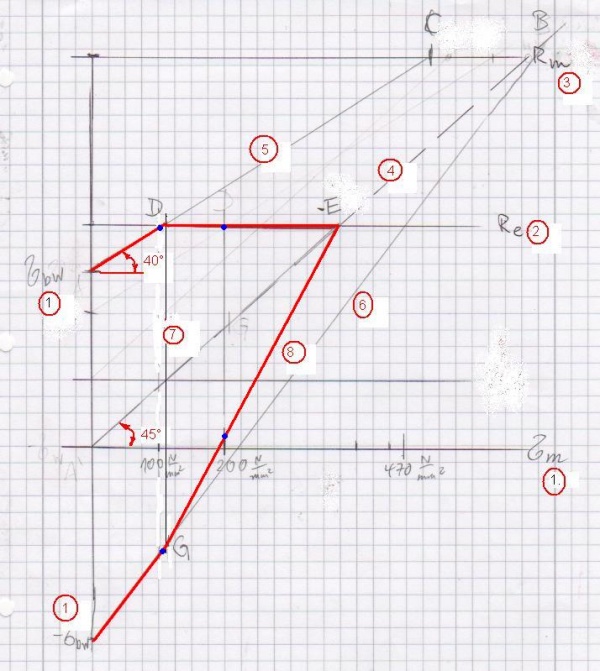
- bei gleichem Maßstab von x- und y-Achse wird auf der x-Achse die Mittelspannung σm eingetragen, auf der y-Achse ±σbw,
- Re parallel zur x-Achse eintragen
- Rm parallel zur x-Achse eintragen
- vom Koordinatenursprung zu Rm eine 45°-Hilfslinie ziehen (Schnittpunkt mit Re ergibt Punkt E)
- eine 40°-Hilfslinie von +σbw zu Rm ziehen (Schnittpunkt mit Re ergibt Punkt D)
- Schnittpunkt von 45°-Hilfslinie und Rm mit -σbw verbinden
- von Punkt D eine Hilfslinie senkrecht nach unten ziehen bis 6 geschnitten wird (ergibt Punkt G)
- Punkte G und E verbinden
- Linien nachziehen von +σbw zu Punkt D, zu Punkt E, zu Punkt G, zu -σbw.
an den blau markierten Punkten auf der roten Kurve, ließt man für a) und b) die folgenden Werte ab:
a) σu= - 155 N/mm²; σo= 330 N/mm²
b) σu= 20 N/mm²; σo= 335 N/mm²
c) Da der Wert 470 N/mm² nicht mehr innerhalb der Kurve liegt, weist der Werkstoff für diese Belastung keine Dauerfestigkeit auf!
zurück zu Festigkeitsberechnung