Kupplungen: Lösung: Unterschied zwischen den Versionen

Aus BS-Wiki: Wissen teilen
Wechseln zu: Navigation, Suche
(→‎Aufgabe 12)
(→‎Aufgabe 10)
 
(21 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 212: Zeile 212:
  
 
b) Rutscht die Kupplung bei verölten Belag (&mu;<sub>H</sub>=0,15), wenn eine Kupplungsdrehkraft (Haftreibungskraft) von mindestens 500N übertragen werden soll?
 
b) Rutscht die Kupplung bei verölten Belag (&mu;<sub>H</sub>=0,15), wenn eine Kupplungsdrehkraft (Haftreibungskraft) von mindestens 500N übertragen werden soll?
 +
 +
 +
für a)
 +
 +
geg:
 +
 +
F<sub>N<sub>je Feder</sub></sub>= 0,35kN
 +
 +
&mu;<sub>H</sub>= 0,35
 +
 +
n<sub>Beläge</sub>= 2
 +
 +
n<sub>Federn</sub>= 8
 +
 +
 +
ges.:
 +
 +
Haftreibungskraft F<sub>R</sub> in N
 +
 +
 +
Lös.:
 +
 +
F<sub>N</sub>= F<sub>N<sub>je Feder</sub></sub> * n<sub>Beläge</sub>
 +
 +
F<sub>N</sub>= 0,35kN * 8
 +
 +
F<sub>N</sub>= <u>2,8kN</u>
 +
 +
 +
lt. Europa Tb. Seite 41
 +
 +
F<sub>R</sub>= F<sub>N</sub> * &mu;<sub>H</sub> * n<sub>Beläge</sub>
 +
 +
F<sub>R</sub>= 2,8kN * 0,35 * 2
 +
 +
F<sub>R</sub>= <u>1,96N</u>
 +
 +
 +
Die Haftreibungskraft beträgt 1960N
 +
 +
 +
 +
für b)
 +
 +
geg:
 +
 +
F<sub>N<sub>je Feder</sub></sub>= 0,35kN
 +
 +
&mu;<sub>H</sub>= 0,15
 +
 +
n<sub>Beläge</sub>= 2
 +
 +
n<sub>Federn</sub>= 8
 +
 +
 +
ges.:
 +
 +
Haftreibungskraft F<sub>R</sub> in N
 +
 +
 +
Lös.:
 +
 +
F<sub>N</sub>= F<sub>N<sub>je Feder</sub></sub> * n<sub>Beläge</sub>
 +
 +
F<sub>N</sub>= 0,35kN * 8
 +
 +
F<sub>N</sub>= <u>2,8kN</u>
 +
 +
 +
lt. Europa Tb. Seite 41
 +
 +
F<sub>R</sub>= F<sub>N</sub> * &mu;<sub>H</sub> * n<sub>Beläge</sub>
 +
 +
F<sub>R</sub>= 2,8kN * 0,35 * 2
 +
 +
F<sub>R</sub>= <u>0,84kN</u>
 +
 +
 +
Nein, die Kupplung rutscht auch bei verölten Belägen nicht, da die tatsächlich erzielte Haftreibungskraft mit 0,84kN die geforderten 0,5kN übertreffen.
  
 
==Aufgabe 10==
 
==Aufgabe 10==
  
−
Eine Einscheibenkupplung muss eine Haftreibungskraft (Drehkraft) von 1kN übertragen. Die Ribungszahl beträgt 0,35. Die verwendeten Druckfedern erzeugen eine Druckkraft (Normalkraft) von je 400N. Wieviele Druckfedern sind mindestens erforderlich.
+
Eine Einscheibenkupplung muss eine Haftreibungskraft (Drehkraft) von 1kN übertragen. Die Ribungszahl beträgt 0,35. Die verwendeten Druckfedern erzeugen eine Druckkraft (Normalkraft) von je 400N. Wie viele Druckfedern sind mindestens erforderlich?
 +
 
 +
 
 +
geg:
 +
 
 +
F<sub>R</sub>= 1kN
 +
 
 +
F<sub>N<sub>je Feder</sub></sub>= 400N
 +
 
 +
&mu;<sub>H</sub>= 0,35
 +
 +
n<sub>Beläge</sub>= 2
 +
 
 +
 
 +
ges.:
 +
 
 +
Anzahl der Federn n<sub>Federn</sub>
 +
 
 +
 
 +
Lös.:
 +
 
 +
lt. Europa Tb. Seite 41
 +
 
 +
F<sub>R</sub>= F<sub>N</sub> * n<sub>Beläge</sub> * &mu;<sub>H</sub>
 +
 
 +
F<sub>N</sub>= F<sub>R</sub> / ( n<sub>Beläge</sub> * &mu;<sub>H</sub> )
 +
 
 +
F<sub>N</sub>= 1000N / ( 2 * 0,35 )
 +
 
 +
F<sub>N</sub>= <u>1428,57N</u>
 +
 
 +
 
 +
n<sub>Federn</sub>= F<sub>N</sub> / F<sub>N<sub>je Feder</sub></sub>
 +
 
 +
n<sub>Federn</sub>= 1428,57N / 400N
 +
 
 +
n<sub>Federn</sub>= <u>3,57</u>
 +
 
 +
 
 +
Es werden mindestens 4 Druckfedern gebraucht.
  
 
==Aufgabe 11==
 
==Aufgabe 11==
  
 
Bei einer Scheibenbremse werden beide Beläge mit einer Anpreßkraft (Normalkraft) von je 3200N an die Reibscheibe gepreßt. Die Gleitreibungszahl beträgt 0,3. Ermittle die Gleitreibungskraft F<sub>G</sub> (Bremskraft) an der Scheibe!
 
Bei einer Scheibenbremse werden beide Beläge mit einer Anpreßkraft (Normalkraft) von je 3200N an die Reibscheibe gepreßt. Die Gleitreibungszahl beträgt 0,3. Ermittle die Gleitreibungskraft F<sub>G</sub> (Bremskraft) an der Scheibe!
 +
 +
 +
geg:
 +
 +
F<sub>N</sub>= 3200N
 +
 +
&mu;<sub>G</sub>= 0,3
 +
 +
n<sub>Beläge</sub>= 2
 +
 +
 +
ges.:
 +
 +
Gleitreibungskraft F<sub>G</sub> in N
 +
 +
 +
Lös.:
 +
 +
lt. Europa Tb. Seite 41
 +
 +
F<sub>G</sub>= F<sub>N</sub> * n<sub>Beläge</sub> * &mu;<sub>G</sub>
 +
 +
F<sub>N</sub>= 3,2kN * 2 * 0,3
 +
 +
F<sub>N</sub>= <u>1,92kN</u>
 +
 +
 +
Die Gleitreibungskraft beträgt 1,92kN
  
 
==Aufgabe 12==
 
==Aufgabe 12==
Zeile 239: Zeile 385:
 
ges:
 
ges:
  
−
Bremsleitungsdruck F<sub>N</sub> in bar
+
Bremsleitungsdruck &sigma;<sub>z</sub> in bar
  
  
Zeile 246: Zeile 392:
 
lt. Europa Tb. Seite 27
 
lt. Europa Tb. Seite 27
  
−
A<sub>s</sub>=  d<sup>2</sup> * &pi; * n<sub>Scheiben</sub>/ 4
+
A<sub>s</sub>=  d<sup>2</sup> * &pi; * n<sub>Scheiben</sub> / 4
  
 
A<sub>s</sub>= 42<sup>2</sup>mm<sup>2</sup> * &pi; * 2 / 4  
 
A<sub>s</sub>= 42<sup>2</sup>mm<sup>2</sup> * &pi; * 2 / 4  
  
−
A<sub>s</sub>= = <u>2770,88mm</u><sup>2</sup>
+
A<sub>s</sub>= <u>2770,88mm</u><sup>2</sup>
 +
 
 +
 
 +
lt. Europa Tb. Seite 41
 +
 
 +
F<sub>G</sub>= F<sub>N</sub> * &mu;<sub>G</sub>
 +
 
 +
F<sub>N</sub>= F<sub>G</sub> / &mu;<sub>G</sub>
 +
 
 +
F<sub>N</sub>= 1500N / 0,35
 +
 
 +
F<sub>N</sub>= <u>4285,714N</u>
 +
 
 +
 
 +
lt. Europa Tb. Seite 45
 +
 
 +
&sigma;<sub>z</sub>= F<sub>N</sub> * A<sub>s</sub>
 +
 
 +
&sigma;<sub>z</sub>= 4285,714N / 2770,88mm<sup>2</sup>
 +
 
 +
&sigma;<sub>z</sub>= <u>1,546N/mm</u><sup>2</sup> = <u>15,46bar</u>
  
  
−
Die Druckkraft der Feder beträgt 250N.
+
Der Bremsleitungsdruck beträgt 15,46bar.
  
 
==Aufgabe 13==
 
==Aufgabe 13==
  
 
Eine Stahlwelle läuft in einem Bronzelager. Die radiale Lagerkraft (Normalkraft) F<sub>N</sub> beträgt 3kN. Berechne die Gleitreibungskraft, wenn die Gleitreibungszahl mit 0,05 angegeben ist.
 
Eine Stahlwelle läuft in einem Bronzelager. Die radiale Lagerkraft (Normalkraft) F<sub>N</sub> beträgt 3kN. Berechne die Gleitreibungskraft, wenn die Gleitreibungszahl mit 0,05 angegeben ist.
 +
 +
 +
geg:
 +
 +
F<sub>N</sub>= 3kN
 +
 +
&mu;<sub>G</sub>= 0,05
 +
 +
 +
ges.:
 +
 +
Gleitreibungskraft F<sub>G</sub> in N
 +
 +
 +
Lös.:
 +
 +
lt. Europa Tb. Seite 41
 +
 +
 +
F<sub>G</sub>= F<sub>N</sub> * &mu;<sub>G</sub>
 +
 +
F<sub>G</sub>= 3000N * 0,05
 +
 +
F<sub>G</sub>= <u>150N</u>
 +
 +
 +
Die Gleitreibungskraft beträgt 150N.
  
 
==Aufgabe 14==
 
==Aufgabe 14==
  
 
Bei einer Außenbackenbremse eines Schwungrades wirken die zwei Beläge mit einer Kraft von je 12000N auf die Trommel. Wie groß ist die Bremskraft F<sub>G</sub> an der Trommel, wenn mit einer Gleitreibungszahl von  &mu;<sub>G</sub>= 0,38 gerechnet werden kann?
 
Bei einer Außenbackenbremse eines Schwungrades wirken die zwei Beläge mit einer Kraft von je 12000N auf die Trommel. Wie groß ist die Bremskraft F<sub>G</sub> an der Trommel, wenn mit einer Gleitreibungszahl von  &mu;<sub>G</sub>= 0,38 gerechnet werden kann?
 +
 +
 +
geg:
 +
 +
F<sub>N</sub>= 12kN
 +
 +
&mu;<sub>G</sub>= 0,38
 +
 +
n<sub>Beläge</sub>= 2
 +
 +
 +
ges.:
 +
 +
Bremskraft F<sub>G</sub> in kN
 +
 +
 +
Lös.:
 +
 +
lt. Europa Tb. Seite 41
 +
 +
F<sub>G</sub>= F<sub>N</sub> * n<sub>Beläge</sub> * &mu;<sub>G</sub>
 +
 +
F<sub>G</sub>= 12kN * 2 * 0,38
 +
 +
F<sub>G</sub>= <u>9,12kN</u>
 +
 +
 +
Die Bremskraft an der Trommel beträgt 9,12kN.
 +
 +
[[Kategorie:Entwicklung und Konstruktion]]

Aktuelle Version vom 22. Mai 2012, 16:00 Uhr

Situation:


Sie machen eine Anfrage für eine Kupplung beim Hersteller, und bekommen einen Tag später ein Angebot über eine Einscheibenkupplung und eine Mehrscheibenkupplung. Treffen sie nun eine Entscheidung, welche der beiden Kupplung für den Einsatz, gefordertes Drehmoment von 170 Nm, am besten geeignet ist. Achten sie hierbei auf das zu übertragende Drehmoment und auf die Sicherheit der jeweiligen Kupplung. Nach den beiden Aufgaben (1 und 2) kann eine Entscheidung über die passende Kupplung getroffen werden!

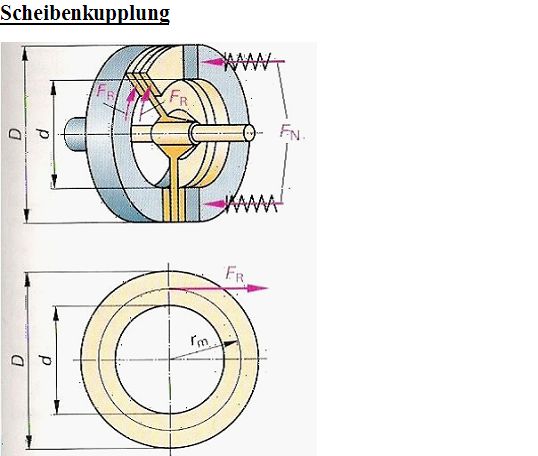
Aufgabe 1

Scheibenkupplung

Geg:
D = 210 mm;
d = 105 mm; z = 1; p = 20 N/cm2;
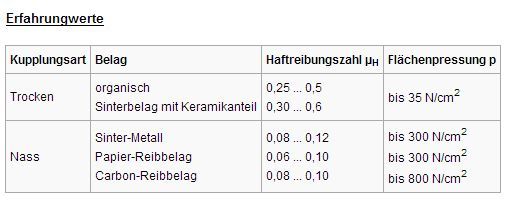
µH = 0,3 (siehe Tabellenwerte);
Mmax = 175,35 Nm.

Ges:
A in cm2;
FN in N;
FR in N;
rm in cm;
Mk in Nm;
die Sicherheitszahl S.

Berechnung:

A = (π / 4) * (D2 - d2)

A = (π / 4) * (212cm2 - 10,52cm2)

A = 259,77cm2

FN = A * p

FN = 259,77 cm2 * 20 N/cm2

FN = 5195,41 N

FR = FN * μH

FR = 5195,41 N * 0,3

FR = 1558,62 N

rm = (D + d) / 4

Erfahrungswerte1.jpg

rm = (21 cm + 10,5 cm) / 4

rm = 7,875 cm

MK = 2 * FR * rm * z

MK = 2 * 1558,62 N * 7,875 cm * 1

MK = 24548,3 Ncm

MK = 245,48 Nm

Formel nach S umstellen.

MK = S * Mmax │

S = MK / Mmax

S = 245,48 Nm / 175,35 Nm

S = 1,4

Aufgabe 2

Begriffserklärung.jpg

Geg:
D = 150 mm;
rm = 5,5 cm;
p = 20 N/cm2;
µH = 0,4 (Siehe Aufgabe);
S = 1,5; z = 2;

Ges:
A in cm2;
d in cm;
Mk in Nm;
Mmax in Nm;
FN in N;
FK in N.


Berechnung:

Formel nach d umstellen.

rm = (D + d) / 4 │

Formeln.jpg

(D + d) / 4 = rm │

(D + d) = rm * 4 │

d = rm * 4 - D

d = 5,5 cm * 4 - 15 cm

d = 7 cm

A = (π / 4) * (D2 - d2)

A = (π / 4) * (152cm2 - 72cm2)

A = 138,23 cm2

FN = A * p

FN = 138,23 cm2 * 20 N/cm2

FN = 2764,6 N

FR = FN * μH

FR = 2764,6 N * 0,4

FR = 1105,84 N

Fk = 2 * FR * z

Fk = 2 * 1105,84 N * 2

Fk = 4423,36 N

MK = Fk * rm

MK = 4423,36 N * 5,5 cm

MK = 24328,49 Ncm

MK = 243,29 Nm

Formel nach Mmax umstellen.

S = MK / Mmax │

MK / Mmax = S │

Mmax = MK / S

Mmax = 243,29 Nm / 1,5

Mmax = 162,2 Nm

Ergebnis:

Nach den ermittelten Werten von der Einscheibenkupplung mit Mmax von 175,35 Nm und der Zweischeibenkupplung mit einen Mmax von 162,2 Nm wird die Einscheibenkupplung als die passendere ausgewählt und bestellt. Die Einscheibenkupplung hat ein maximal übertragbares Drehmoment von 175,35 Nm und liegt über den geforderten Wert von 170 Nm. 170 Nm < 175,35 Nm
Die Sicherheit der Einscheibenkupplung beträgt S = 1,4 und liegt unter der Sicherheit der Zweischeibenkupplung (S = 1,5).


Aufgabe 7

Die Anpresskraft (Normalkraft) FN eines Reibbellages bei einer Einscheibenkupplung beträgt 4,2kN. Die Reibungszahl ist 0,35. Ermittele die Haftreibungskraft bei 2 Belagseiten!


geg:

FN= 4,2kN

μH= 0,35

n= 2 (Belagsseiten)


ges:

Haftreibungskraft FR in kN


Lös:

lt. Europa Tb. Seite 41

FR= FN * μH * n

FR= 0,35 * 4,2kN * 2

FR=2,94kN


Die Haftreibungskraft beträgt 2,94kN.

Aufgabe 8

Eine Einscheibenkupplung (2 Belagseiten) soll eine Haftreibungskraft von 1,8kN übertragen. Die Reibungszahl beträgt 0,3. Die Anpresskraft (Normalkraft) FN wird von 12 Kupplungsdruckfedern erzeugt. Ermittle die Druckkraft einer Feder!


geg:

FR= 4,2kN

μH= 0,3

nBelag= 2

nFedern= 12


ges:

Haftreibungskraft FN in kN


Lös:

lt. Europa Tb. Seite 41

FR = FN / nFedern * ( μH * nBelag )

FN / nFedern = FR / ( μH * nBelag )

FN / 12 = 1800N / 0,3 * 2

FN = 250N


Die Druckkraft der Feder beträgt 250N.

Aufgabe 9

Bei einer Einscheibenkupplung (2 Belagseiten) erzeugen 8 Druckfedern die erforderliche Anpreßkraft (Normalkraft). Jede Feder hat eine Druckkraft von 350N. Die Reibungszahl μH beträgt 0,35.

a) Wie groß ist die Haftreibungskraft (Kupplungsdrehkraft)?

b) Rutscht die Kupplung bei verölten Belag (μH=0,15), wenn eine Kupplungsdrehkraft (Haftreibungskraft) von mindestens 500N übertragen werden soll?


für a)

geg:

FNje Feder= 0,35kN

μH= 0,35

nBeläge= 2

nFedern= 8


ges.:

Haftreibungskraft FR in N


Lös.:

FN= FNje Feder * nBeläge

FN= 0,35kN * 8

FN= 2,8kN


lt. Europa Tb. Seite 41

FR= FN * μH * nBeläge

FR= 2,8kN * 0,35 * 2

FR= 1,96N


Die Haftreibungskraft beträgt 1960N


für b)

geg:

FNje Feder= 0,35kN

μH= 0,15

nBeläge= 2

nFedern= 8


ges.:

Haftreibungskraft FR in N


Lös.:

FN= FNje Feder * nBeläge

FN= 0,35kN * 8

FN= 2,8kN


lt. Europa Tb. Seite 41

FR= FN * μH * nBeläge

FR= 2,8kN * 0,35 * 2

FR= 0,84kN


Nein, die Kupplung rutscht auch bei verölten Belägen nicht, da die tatsächlich erzielte Haftreibungskraft mit 0,84kN die geforderten 0,5kN übertreffen.

Aufgabe 10

Eine Einscheibenkupplung muss eine Haftreibungskraft (Drehkraft) von 1kN übertragen. Die Ribungszahl beträgt 0,35. Die verwendeten Druckfedern erzeugen eine Druckkraft (Normalkraft) von je 400N. Wie viele Druckfedern sind mindestens erforderlich?


geg:

FR= 1kN

FNje Feder= 400N

μH= 0,35

nBeläge= 2


ges.:

Anzahl der Federn nFedern


Lös.:

lt. Europa Tb. Seite 41

FR= FN * nBeläge * μH

FN= FR / ( nBeläge * μH )

FN= 1000N / ( 2 * 0,35 )

FN= 1428,57N


nFedern= FN / FNje Feder

nFedern= 1428,57N / 400N

nFedern= 3,57


Es werden mindestens 4 Druckfedern gebraucht.

Aufgabe 11

Bei einer Scheibenbremse werden beide Beläge mit einer Anpreßkraft (Normalkraft) von je 3200N an die Reibscheibe gepreßt. Die Gleitreibungszahl beträgt 0,3. Ermittle die Gleitreibungskraft FG (Bremskraft) an der Scheibe!


geg:

FN= 3200N

μG= 0,3

nBeläge= 2


ges.:

Gleitreibungskraft FG in N


Lös.:

lt. Europa Tb. Seite 41

FG= FN * nBeläge * μG

FN= 3,2kN * 2 * 0,3

FN= 1,92kN


Die Gleitreibungskraft beträgt 1,92kN

Aufgabe 12

Die Bremskolbendurchmesser einer Scheibenbremse beträgt 42mm. Die Gleitreibungskraft FG (Bremskraft) an der Scheibe soll bei einer Gleitreibungszahl von 0,35, 1500N betragen. Ermittle den Bremsleitungsdruck! (1bar=10N/cm2)


geg:

d= 42mm

FG= 1500N

μG= 0,35

nScheiben= 2


ges:

Bremsleitungsdruck σz in bar


Lös:

lt. Europa Tb. Seite 27

As= d2 * π * nScheiben / 4

As= 422mm2 * π * 2 / 4

As= 2770,88mm2


lt. Europa Tb. Seite 41

FG= FN * μG

FN= FG / μG

FN= 1500N / 0,35

FN= 4285,714N


lt. Europa Tb. Seite 45

σz= FN * As

σz= 4285,714N / 2770,88mm2

σz= 1,546N/mm2 = 15,46bar


Der Bremsleitungsdruck beträgt 15,46bar.

Aufgabe 13

Eine Stahlwelle läuft in einem Bronzelager. Die radiale Lagerkraft (Normalkraft) FN beträgt 3kN. Berechne die Gleitreibungskraft, wenn die Gleitreibungszahl mit 0,05 angegeben ist.


geg:

FN= 3kN

μG= 0,05


ges.:

Gleitreibungskraft FG in N


Lös.:

lt. Europa Tb. Seite 41


FG= FN * μG

FG= 3000N * 0,05

FG= 150N


Die Gleitreibungskraft beträgt 150N.

Aufgabe 14

Bei einer Außenbackenbremse eines Schwungrades wirken die zwei Beläge mit einer Kraft von je 12000N auf die Trommel. Wie groß ist die Bremskraft FG an der Trommel, wenn mit einer Gleitreibungszahl von μG= 0,38 gerechnet werden kann?


geg:

FN= 12kN

μG= 0,38

nBeläge= 2


ges.:

Bremskraft FG in kN


Lös.:

lt. Europa Tb. Seite 41

FG= FN * nBeläge * μG

FG= 12kN * 2 * 0,38

FG= 9,12kN


Die Bremskraft an der Trommel beträgt 9,12kN.

Abgerufen von „http://bs-wiki.de/mediawiki/index.php?title=Kupplungen:_Lösung&oldid=63191“