Logarithmus: Unterschied zwischen den Versionen
Aus BS-Wiki: Wissen teilen
Dg (Diskussion | Beiträge) |
Dg (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| − | {| | + | {| |
| − | |[[Bild:Logarithmus.gif]] ||Der '''Logarithmus''' log ist die Umkehrfunktion des Potenzierens. Der Zusammenhang beider Funktionen ist im Bild veranschaulicht. Als Definition für den Logarithmus gilt entsprechend: | + | |[[Bild:Logarithmus.gif]] || || {{navi|Zehn hoch|Eulersche Zahl}} |
| + | Der '''Logarithmus''' log ist die Umkehrfunktion des Potenzierens. Der Zusammenhang beider Funktionen ist im Bild veranschaulicht. Als Definition für den Logarithmus gilt entsprechend: | ||
'''''Der Logarithmus ist die Zahl, mit der ich die Basis potenzieren muss, um den Numerus bzw. Potenzwert zu erhalten.''''' | '''''Der Logarithmus ist die Zahl, mit der ich die Basis potenzieren muss, um den Numerus bzw. Potenzwert zu erhalten.''''' | ||
| Zeile 9: | Zeile 10: | ||
* natürlicher Logarithmus zur Basis [[Eulersche Zahl|e]], kurz ln | * natürlicher Logarithmus zur Basis [[Eulersche Zahl|e]], kurz ln | ||
| − | Umrechnung: log<sub>10</sub>x = 2,3026{{*}}ln x | + | Umrechnung: log<sub>10</sub> x = 2,3026{{*}}ln x |
| − | |||
| − | |||
|} | |} | ||
Version vom 23. März 2011, 19:54 Uhr
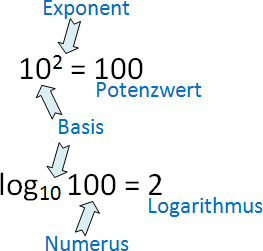 |
Der Logarithmus log ist die Umkehrfunktion des Potenzierens. Der Zusammenhang beider Funktionen ist im Bild veranschaulicht. Als Definition für den Logarithmus gilt entsprechend: Der Logarithmus ist die Zahl, mit der ich die Basis potenzieren muss, um den Numerus bzw. Potenzwert zu erhalten. Im Prinzip ist jede Basis denkbar, bei technischen Berechnungen werden i.d.R. nur zwei Logarithmen verwendet:
Umrechnung: log10 x = 2,3026 · ln x | ||||||||||