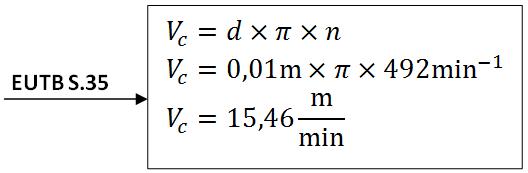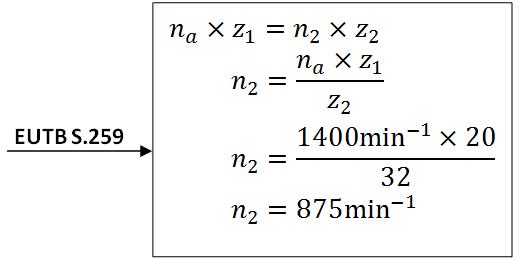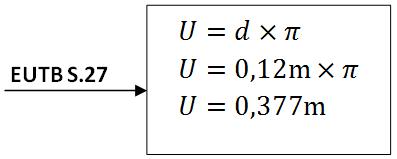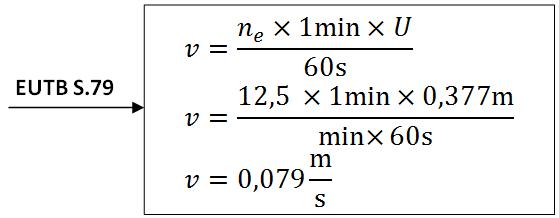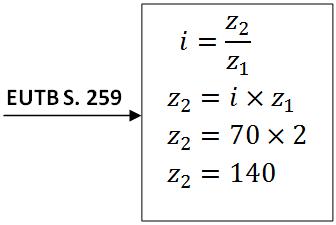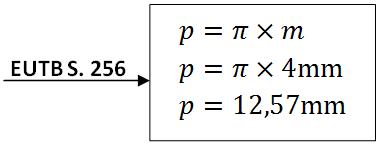Zahnräder und Zahnradgetriebe: Lösungen: Unterschied zwischen den Versionen
(→Seiltrommelantrieb) |
(→Lösung Frage 1) |
||
| (55 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 24: | Zeile 24: | ||
Die Schnittgeschwindigkeit des 10mm Bohrers beträgt V<sub>c</sub>=15,46m/min.<br /> | Die Schnittgeschwindigkeit des 10mm Bohrers beträgt V<sub>c</sub>=15,46m/min.<br /> | ||
<br /> | <br /> | ||
| + | <br /> | ||
| + | [[Media:Zahnräder und Zahnradgetriebe Zweigang-Bohrmaschine.pdf|Druckversion der Aufgabe]]<br /> | ||
<br /> | <br /> | ||
[[ Zahnräder und Zahnradgetriebe#Zweigang-Bohrmaschine|Rückkehr zum Hauptartikel]]<br /> | [[ Zahnräder und Zahnradgetriebe#Zweigang-Bohrmaschine|Rückkehr zum Hauptartikel]]<br /> | ||
| Zeile 38: | Zeile 40: | ||
e) Die Zähnezahl des Schneckenrades z<sub>4</sub> | e) Die Zähnezahl des Schneckenrades z<sub>4</sub> | ||
<br /> | <br /> | ||
| − | |||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | <br /><br /> | ||
| + | Rechenweg:<br /> | ||
<br /> | <br /> | ||
| − | + | gegeben: a/b/c/d/e) na = 1400 min<sup>-1</sup> ; z<sub>1</sub> = 20 ; z<sub>2</sub> = 32 ; z<sub>3</sub> = 2 ; Trommel Ø120mm ; i<sub>2</sub> = 70:1<br /> | |
| − | |||
| + | gesucht: a) n<sub>2</sub> = ?<br /> | ||
| + | a) Ermitteln der Schneckenwellendrehfrequenz<br /> | ||
| + | [[Bild:Zahnräder_Seiltrommelantrieb1.jpg|center]]<br /> | ||
| + | Die Welle der Schnecke dreht sich mit 875 min<sup>-1</sup> <br /> | ||
| + | <br /> | ||
| + | gesucht: b)n<sub>e</sub> = ?<br /> | ||
| + | b) Seiltrommeldrehfrequenz ermitteln<br /> | ||
| − | [[ | + | [[Bild:Zahnräder_Seiltrommelantrieb2.jpg|center]]<br /> |
| + | Die Drehfrequenz der Seiltrommel ist n<sub>e</sub>=12,5min<sup>-1</sup><br /> | ||
<br /> | <br /> | ||
| + | |||
| + | gesucht: c) v = ?<br /> | ||
| + | c) Umfang der Seiltrommel berechnen<br /> | ||
| + | |||
| + | [[Bild:Zahnräder_Seiltrommelantrieb3.jpg|center]]<br /> | ||
| + | |||
| + | Geschwindigkeit der Seiltrommel berechnen<br /> | ||
| + | |||
| + | [[Bild:Zahnräder_Seiltrommelantrieb4.jpg|center]]<br /> | ||
| + | |||
| + | Das Seil wird mit 0,079m/s auf die Seiltrommel aufgerollt.<br /> | ||
<br /> | <br /> | ||
| + | |||
| + | gesucht: d) a = ?<br /> | ||
| + | d) Teilkreisdurchmesser bestimmen<br /> | ||
| + | |||
| + | [[Bild:Zahnräder_Seiltrommelantrieb5.jpg|center]]<br /> | ||
| + | |||
| + | Wellenabstand bestimmen<br /> | ||
| + | |||
| + | [[Bild:Zahnräder_Seiltrommelantrieb6.jpg|center]]<br /> | ||
| + | |||
| + | Der Wellenabstand „a“ ist 104mm<br /> | ||
<br /> | <br /> | ||
| + | |||
| + | gesucht: e) z<sub>4</sub> = ?<br /> | ||
| + | e) Zähnezahl berechnen<br /> | ||
| + | |||
| + | [[Bild:Zahnräder_Seiltrommelantrieb7.jpg|center]]<br /> | ||
| + | |||
| + | Das Schneckenzahnrad hat 140 Zähne.<br /> | ||
<br /> | <br /> | ||
| + | [[Media:Zahnräder und Zahnradgetriebe Seiltrommelantrieb.pdf|Druckversion der Aufgabe]] | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | + | [[ Zahnräder und Zahnradgetriebe#Seiltrommelantrieb|Rückkehr zum Hauptartikel]]<br /> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <br /> | ||
== Zahnstangenantrieb == | == Zahnstangenantrieb == | ||
| Zeile 74: | Zeile 106: | ||
Eine Zahnstange wird durch ein Zahnrad mit z = 32 angetrieben. Modul m = 4mm.<br /> | Eine Zahnstange wird durch ein Zahnrad mit z = 32 angetrieben. Modul m = 4mm.<br /> | ||
Wie groß ist der Hub der Zahnstange bei einer Zahnradumdrehung?<br /> | Wie groß ist der Hub der Zahnstange bei einer Zahnradumdrehung?<br /> | ||
| + | <br /> | ||
| + | <br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Zeile 80: | Zeile 114: | ||
Rechenweg:<br /> | Rechenweg:<br /> | ||
<br /> | <br /> | ||
| + | gegeben: z = 32 ; m = 4mm<br /> | ||
| + | gesucht: d<sub>1</sub> = ?<br /> | ||
<br /> | <br /> | ||
| − | <br /> | + | Zahnradteilung ausrechnen<br /> |
| − | [[ | + | |
| + | [[Bild:Zahnräder_Zahnstangenantrieb1.jpg|center]]<br /> | ||
| + | |||
| + | Teilkreisdurchmesser berechnen<br /> | ||
| + | |||
| + | [[Bild:Zahnräder_Zahnstangenantrieb2.jpg|center]]<br /> | ||
| + | Der Hub der Zahnstange beträgt 402,24mm bei einer Umdrehung des Zahnrades.<br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | [[Media:Zahnräder und Zahnradgetriebe Zahnstangenantrieb.pdf| Druckversion der Aufgabe]]<br /> | ||
<br /> | <br /> | ||
| − | + | [[ Zahnräder und Zahnradgetriebe#Zahnstangenantrieb|Rückkehr zum Hauptartikel]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Tischverstellung == | == Tischverstellung == | ||
| Zeile 113: | Zeile 145: | ||
Rechenweg:<br /> | Rechenweg:<br /> | ||
<br /> | <br /> | ||
| + | gegeben: a/b) z<sub>1</sub> = 27 ; z<sub>2</sub> = 18 ; Tr12x3 (p = 3mm) ; l<sub>1</sub> = 36mm<br /> | ||
| + | gesucht: a) n<sub>e</sub> = ? (Umdrehungen)<br /> | ||
<br /> | <br /> | ||
| − | [[ | + | a) Trapezwellenumdrehungen berechnen<br /> |
| − | + | ||
| − | <br /> | + | [[Bild:Zahnräder_Tischverstellung1.jpg|center]]<br /> |
| − | + | ||
| − | + | Kurbelumdrehungen berechnen<br /> | |
| − | <br /> | + | |
| − | + | [[Bild:Zahnräder_Tischverstellung2.jpg|center]]<br /> | |
| − | <br /> | + | |
| − | <br /> | + | Die Handkurbel muss 8 mal gedreht werden, um einen Weg von 36mm zurückzulegen.<br /> |
| − | < | + | <br /> |
| − | < | + | gesucht: b) l<sub>2</sub> = ?<br /> |
| − | <br /> | ||
<br /> | <br /> | ||
| + | |||
| + | b) Übersetzungsverhältnis berechnen<br /> | ||
| + | |||
| + | [[Bild:Zahnräder_Tischverstellung3.jpg|center]]<br /> | ||
| + | |||
| + | l<sub>2</sub> berechnen<br /> | ||
| + | |||
| + | [[Bild:Zahnräder_Tischverstellung4.jpg|center]]<br /> | ||
| + | |||
| + | Die Trapezspindel bewegt den Tisch um 4,5 mm bei einer Kurbelumdrehung.<br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | [[Media:Zahnräder und Zahnradgetriebe Tischverstellung.pdf| Druckversion der Aufgabe]]<br /> | ||
<br /> | <br /> | ||
| + | [[ Zahnräder und Zahnradgetriebe#Tischverstellung|Rückkehr zum Hauptartikel]]<br /> | ||
== Übersetzung == | == Übersetzung == | ||
| Zeile 144: | Zeile 189: | ||
Rechenweg:<br /> | Rechenweg:<br /> | ||
<br /> | <br /> | ||
| + | gegeben: a/b/c) n<sub>a</sub> = 1440 min<sup>-1</sup> ; n<sub>e</sub> = 192 min<sup>-1</sup> ; z<sub>1</sub> = 18 ; z<sub>2</sub> = 45 ; z<sub>4</sub> = 42<br /> | ||
| + | gesucht: a) i<sub>ges</sub> = ? <br /> | ||
| + | <br /> | ||
| + | a) Gesamtübersetzungsverhältnis berechnen<br /> | ||
| + | [[Bild:Zahnräder_Übersetzung1.jpg|center]]<br /> | ||
| − | + | Das Gesamtübersetzungsverhältnis ist i<sub>ges</sub>=7,5.<br /> | |
| − | |||
| − | < | ||
| − | <br /> | ||
<br /> | <br /> | ||
| + | |||
| + | gesucht: b) i<sub>1</sub> = ? ; i<sub>2</sub> = ?<br /> | ||
<br /> | <br /> | ||
| + | b) Einzelübersetzungen berechnen<br /> | ||
| + | |||
| + | |||
| + | [[Bild:Zahnräder_Übersetzung2.jpg|center]]<br /> | ||
| + | |||
| + | Die Einzelübersetzungsverhältnisse betragen i<sub>1</sub>=2,5 und i<sub>2</sub>=3 <br /> | ||
<br /> | <br /> | ||
| + | Gesucht: c) z<sub>3</sub> = ?<br /> | ||
<br /> | <br /> | ||
| + | c) Zähnezahl des Zahnrades z<sub>3</sub> berechnen<br /> | ||
| + | |||
| + | [[Bild:Zahnräder_Übersetzung3.jpg|center]]<br /> | ||
| + | |||
| + | Das Zahnrad hat 14 Zähne.<br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | [[Media:Zahnräder und Zahnradgetriebe Übersetzung.pdf| Druckversion der Aufgabe]]<br /> | ||
<br /> | <br /> | ||
| + | [[ Zahnräder und Zahnradgetriebe#Übersetzung|Rückkehr zum Hauptartikel]]<br /> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | |||
| + | == Lösung Frage 1 == | ||
| + | Frage:<br /> | ||
| + | Welche Unterschiede gibt es bei Zahnradgetrieben und was sind ihre Vor- und Nachteile? <br /> | ||
<br /> | <br /> | ||
| + | Antwort:<br /> | ||
| + | Es gibt offene und geschlossene Getriebe wobei die geschlossenen überwiegen. Die Vorteile der Zahnradgetriebe sind ein hoher Wirkungsgrad bei Kompakter Bauweise. Nachteilig ist da Zahnradgetriebe ihr Kraft durch Formschluss übertragen müssen elastische Kupplungen vorgesehen werden. Unerwünschte Schwingungen können durch bessere Verzahnungsqualität reduziert werden. | ||
| + | <br /><br /> | ||
| + | |||
| + | [[ Zahnräder und Zahnradgetriebe#Funktion und Wirkung |Rückkehr zum Hauptartikel]]<br /> | ||
| + | |||
| + | == Lösung Frage 2 == | ||
| + | Frage:<br /> | ||
| + | Welche unterschiede gibt es zwischen der Evolventen und Zykloidenverzahnung im Bezug auf die Eingriffslinie?<br /> | ||
<br /> | <br /> | ||
| + | Antwort:<br /> | ||
| + | Die Eingriffslinie stellt bei der Evolventenverzahung eine Gerade dar. Sie liegt an jedem Zahnrad am Grundkreis an. Dadurch das die Eingrifsstrecke eine Gerade ist sind die Zahnräder unempfindlich gegen Achsabstandsänderungen. Bei der Zykloidenverzahnung setzt sich die Eingriffstrecke aus den Bögen der Rollkreise zusammen. Zwei Zahnräder gehören immer als Satz zusammen. Will man Wechselräder oder Schieberäder realisieren, geht dies nur unter Verwendung gleicher Rollkreise.<br /> | ||
<br /> | <br /> | ||
| + | [[ Zahnräder und Zahnradgetriebe#Flankenprofile und Verzahnungsarten|Rückkehr zum Hauptartikel]]<br /> | ||
| + | |||
| + | |||
| + | [[Kategorie:Entwicklung und Konstruktion]] | ||
Aktuelle Version vom 11. Oktober 2008, 22:19 Uhr
Inhaltsverzeichnis
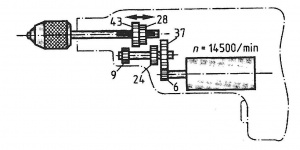
Zweigang-Bohrmaschine
Aufgabe
Für die abgebildete Bohrmaschine sollen folgende Werte berechnet werden:
Die Drehzahlen der Bohrspindel
Die Schnittgeschwindigkeit bei einem Bohrerdurchmesser von 10mm bei niederster Drehzahl.
Rechenweg:
gegeben: a/b) z1 = 6 ; z2 = 37 ; z3 = 24 ; z4 = 28 ; z5 = 9 ; z6 = 43 ; na = 14500min-1 ; Bohrer Ø10mm
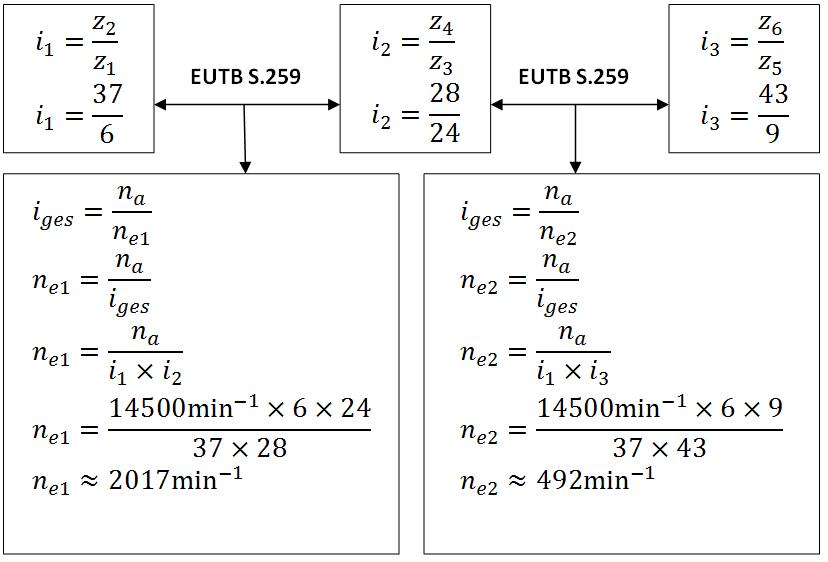
gesucht: a) ne1 = ? ; ne2 = ?
a) Ermitteln der Drehfrequenzen ne1 und ne2
Die Drehfrequenzen der Bohrmaschine sind ne1 ≈ 2017 min-1 und ne2 ≈ 492 min-1.
gesucht: b) Vc = ?
b) ermitteln der Schnittgeschwindigkeit
Die Schnittgeschwindigkeit des 10mm Bohrers beträgt Vc=15,46m/min.
Druckversion der Aufgabe
Rückkehr zum Hauptartikel
Seiltrommelantrieb
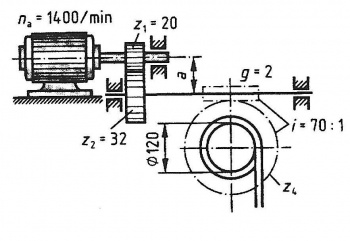
Aufgabe:
Für den Seiltrommelantrieb müssen folgende Berechnungen durchgeführt werden:
a) Die Drehfrequenz der Schnecke
b) Die Drehfrequenz der Seiltrommel
c) Die Geschwindigkeit des Seiles in m/s
d) Den Achsabstand a bei Modul m = 4mm
e) Die Zähnezahl des Schneckenrades z4
Rechenweg:
gegeben: a/b/c/d/e) na = 1400 min-1 ; z1 = 20 ; z2 = 32 ; z3 = 2 ; Trommel Ø120mm ; i2 = 70:1
gesucht: a) n2 = ?
a) Ermitteln der Schneckenwellendrehfrequenz
Die Welle der Schnecke dreht sich mit 875 min-1
gesucht: b)ne = ?
b) Seiltrommeldrehfrequenz ermitteln
Die Drehfrequenz der Seiltrommel ist ne=12,5min-1
gesucht: c) v = ?
c) Umfang der Seiltrommel berechnen
Geschwindigkeit der Seiltrommel berechnen
Das Seil wird mit 0,079m/s auf die Seiltrommel aufgerollt.
gesucht: d) a = ?
d) Teilkreisdurchmesser bestimmen
Wellenabstand bestimmen
Der Wellenabstand „a“ ist 104mm
gesucht: e) z4 = ?
e) Zähnezahl berechnen
Das Schneckenzahnrad hat 140 Zähne.
Druckversion der Aufgabe
Rückkehr zum Hauptartikel
Zahnstangenantrieb
Aufgabe:
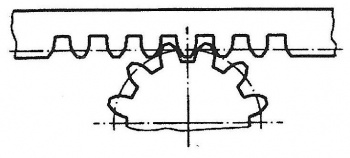
Eine Zahnstange wird durch ein Zahnrad mit z = 32 angetrieben. Modul m = 4mm.
Wie groß ist der Hub der Zahnstange bei einer Zahnradumdrehung?
Rechenweg:
gegeben: z = 32 ; m = 4mm
gesucht: d1 = ?
Zahnradteilung ausrechnen
Teilkreisdurchmesser berechnen
Der Hub der Zahnstange beträgt 402,24mm bei einer Umdrehung des Zahnrades.
Druckversion der Aufgabe
Rückkehr zum Hauptartikel
Tischverstellung
Aufgabe:
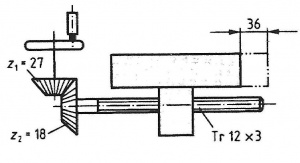
Ein Tisch einer Maschine kann wie in der Abbildung verstellt werden. Berechnen Sie:
a) Die Zahl der Kurbelumdrehungen für einen Weg von 36 mm
b) Den Weg bei einer Umdrehung der Kurbel.
Rechenweg:
gegeben: a/b) z1 = 27 ; z2 = 18 ; Tr12x3 (p = 3mm) ; l1 = 36mm
gesucht: a) ne = ? (Umdrehungen)
a) Trapezwellenumdrehungen berechnen
Kurbelumdrehungen berechnen
Die Handkurbel muss 8 mal gedreht werden, um einen Weg von 36mm zurückzulegen.
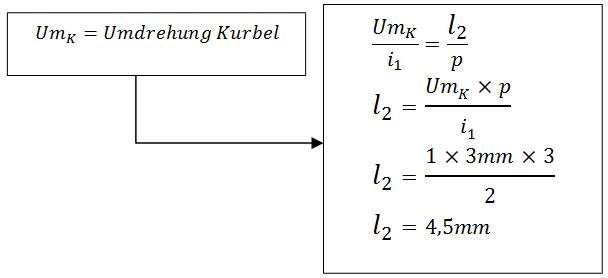
gesucht: b) l2 = ?
b) Übersetzungsverhältnis berechnen
l2 berechnen
Die Trapezspindel bewegt den Tisch um 4,5 mm bei einer Kurbelumdrehung.
Druckversion der Aufgabe
Rückkehr zum Hauptartikel
Übersetzung
Aufgabe:
Ein Elektromotor treibt über ein zweistufiges Zahnradgetriebe eine Säge an. Die Motor-drehfrequenz ist 1440 min-1, die Säge hat eine Drehfrequenz von 192 min-1. Die Zahnräder der ersten Stufe haben z1 = 18 und z2 = 45 Zähne. Das Zahnrad z4 hat 42 Zähne.
Berechnen Sie:
a) Die Gesamtübersetzung
b) Die Einzelübersetzungen
c) Die Zähnezahl des Zahnrades z3
Rechenweg:
gegeben: a/b/c) na = 1440 min-1 ; ne = 192 min-1 ; z1 = 18 ; z2 = 45 ; z4 = 42
gesucht: a) iges = ?
a) Gesamtübersetzungsverhältnis berechnen
Das Gesamtübersetzungsverhältnis ist iges=7,5.
gesucht: b) i1 = ? ; i2 = ?
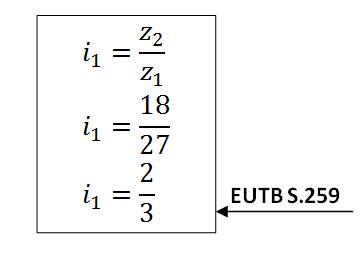
b) Einzelübersetzungen berechnen
Die Einzelübersetzungsverhältnisse betragen i1=2,5 und i2=3
Gesucht: c) z3 = ?
c) Zähnezahl des Zahnrades z3 berechnen
Das Zahnrad hat 14 Zähne.
Druckversion der Aufgabe
Rückkehr zum Hauptartikel
Lösung Frage 1
Frage:
Welche Unterschiede gibt es bei Zahnradgetrieben und was sind ihre Vor- und Nachteile?
Antwort:
Es gibt offene und geschlossene Getriebe wobei die geschlossenen überwiegen. Die Vorteile der Zahnradgetriebe sind ein hoher Wirkungsgrad bei Kompakter Bauweise. Nachteilig ist da Zahnradgetriebe ihr Kraft durch Formschluss übertragen müssen elastische Kupplungen vorgesehen werden. Unerwünschte Schwingungen können durch bessere Verzahnungsqualität reduziert werden.
Lösung Frage 2
Frage:
Welche unterschiede gibt es zwischen der Evolventen und Zykloidenverzahnung im Bezug auf die Eingriffslinie?
Antwort:
Die Eingriffslinie stellt bei der Evolventenverzahung eine Gerade dar. Sie liegt an jedem Zahnrad am Grundkreis an. Dadurch das die Eingrifsstrecke eine Gerade ist sind die Zahnräder unempfindlich gegen Achsabstandsänderungen. Bei der Zykloidenverzahnung setzt sich die Eingriffstrecke aus den Bögen der Rollkreise zusammen. Zwei Zahnräder gehören immer als Satz zusammen. Will man Wechselräder oder Schieberäder realisieren, geht dies nur unter Verwendung gleicher Rollkreise.
Rückkehr zum Hauptartikel