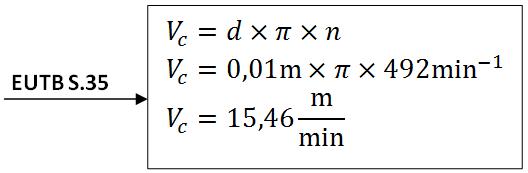Zahnräder und Zahnradgetriebe: Lösungen: Unterschied zwischen den Versionen

Version vom 11. Oktober 2008, 00:08 Uhr

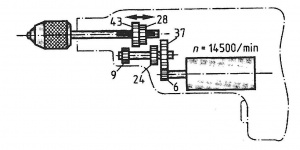
Zweigang-Bohrmaschine

Aufgabe

Für die abgebildete Bohrmaschine sollen folgende Werte berechnet werden:
Die Drehzahlen der Bohrspindel
Die Schnittgeschwindigkeit bei einem Bohrerdurchmesser von 10mm bei niederster Drehzahl.





Rechenweg:
gegeben: a/b) z₁ = 6 ; z₂ = 37 ; z₃ = 24 ; z₄ = 28 ; z₅ = 9 ; z₆ = 43 ; n_a = 14500min^-1 ; Bohrer Ø10mm
gesucht: a) n_e1 = ? ; n_e2 = ?
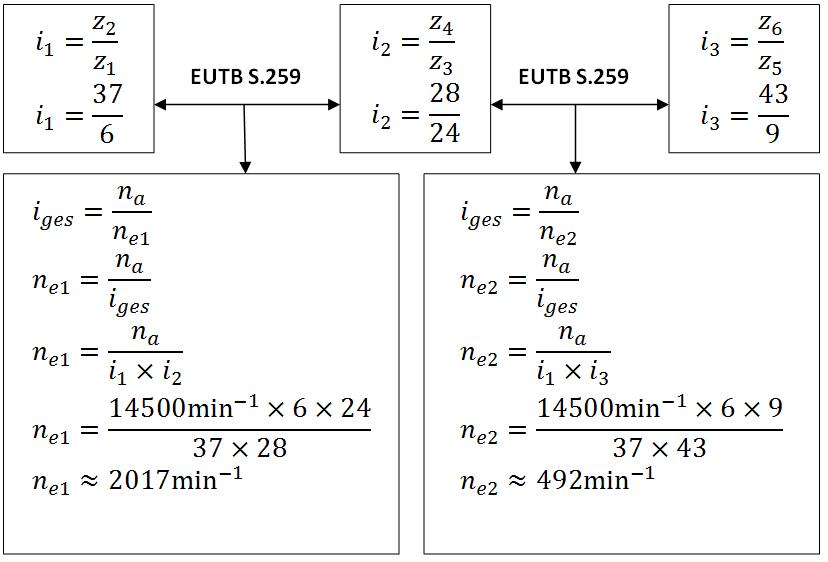
a) Ermitteln der Drehfrequenzen ne1 und ne2

Die Drehfrequenzen der Bohrmaschine sind n_e1 ≈ 2017 min^-1 und n_e2 ≈ 492 min^-1.

gesucht: b) Vc = ?
b) ermitteln der Schnittgeschwindigkeit

Die Schnittgeschwindigkeit des 10mm Bohrers beträgt V_c=15,46m/min.


Rückkehr zum Hauptartikel

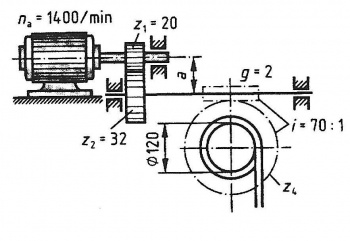
Seiltrommelantrieb

Aufgabe:

Für den Seiltrommelantrieb müssen folgende Berechnungen durchgeführt werden:
a) Die Drehfrequenz der Schnecke
b) Die Drehfrequenz der Seiltrommel
c) Die Geschwindigkeit des Seiles in m/s
d) Den Achsabstand a bei Modul m = 4mm
e) Die Zähnezahl des Schneckenrades z₄
Rechenweg:



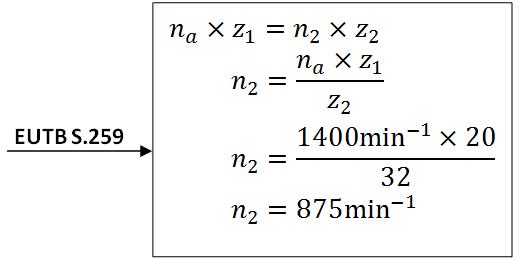Rückkehr zum Hauptartikel

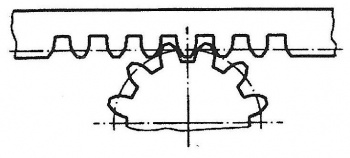
Zahnstangenantrieb

Aufgabe:

Eine Zahnstange wird durch ein Zahnrad mit z = 32 angetrieben. Modul m = 4mm.
Wie groß ist der Hub der Zahnstange bei einer Zahnradumdrehung?




Rechenweg:



Rückkehr zum Hauptartikel

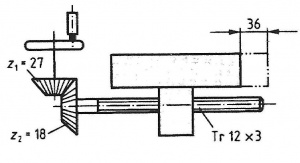
Tischverstellung

Aufgabe:

Ein Tisch einer Maschine kann wie in der Abbildung verstellt werden. Berechnen Sie:

a) Die Zahl der Kurbelumdrehungen für einen Weg von 36 mm
b) Den Weg bei einer Umdrehung der Kurbel.




Rechenweg:


Rückkehr zum Hauptartikel

Übersetzung

Aufgabe:
Ein Elektromotor treibt über ein zweistufiges Zahnradgetriebe eine Säge an. Die Motor-drehfrequenz ist 1440 min^-1, die Säge hat eine Drehfrequenz von 192 min^-1. Die Zahnräder der ersten Stufe haben z₁ = 18 und z₂ = 45 Zähne. Das Zahnrad z₄ hat 42 Zähne.
Berechnen Sie:
a) Die Gesamtübersetzung
b) Die Einzelübersetzungen
c) Die Zähnezahl des Zahnrades z3



Rechenweg:

Rückkehr zum Hauptartikel