Bolzen- und Stiftverbindungen: Lösung: Unterschied zwischen den Versionen
Bülent (Diskussion | Beiträge) (→'''b-)''') |
Bülent (Diskussion | Beiträge) (→'''b-)''') |
||
| Zeile 94: | Zeile 94: | ||
Für die größte Schubspannung in der Nulllinie des Bolzens gilt nach Gl.9.3: | Für die größte Schubspannung in der Nulllinie des Bolzens gilt nach Gl.9.3: | ||
| − | '''τ'''<sub>max</sub> ≈ 4/3 * [ (KA*Fnenn) / (As*2) ] < '''τa'''<sub>zul</sub> (Gl.9.3) | + | {{Mark |
| + | |'''τ'''<sub>max</sub> ≈ 4/3 * [ (KA*Fnenn) / (As*2) ] < '''τa'''<sub>zul</sub>}} (Gl.9.3) | ||
<span style="color: red">Anwendungsfaktor KA = 2,5 wie a-)</span> | <span style="color: red">Anwendungsfaktor KA = 2,5 wie a-)</span> | ||
| Zeile 100: | Zeile 101: | ||
<u>d = 25 mm</u> | <u>d = 25 mm</u> | ||
| − | Bolzenquerschnittsfläche As = 25² mm² *π / 4 | + | Bolzenquerschnittsfläche As = (25² mm² *π) / 4 |
<u>As = 490,87 mm²</u> | <u>As = 490,87 mm²</u> | ||
| Zeile 114: | Zeile 115: | ||
'''τa'''<sub>zul</sub> = <u>60 N/ mm²</u> | '''τa'''<sub>zul</sub> = <u>60 N/ mm²</u> | ||
| − | + | '''τa'''<sub>zul</sub> = 60 N/ mm² > τmax = 49,23 N/ mm² | |
Für die mittlere Flächenpressung in der Gabelbohrung gilt nach Gl.9.4: | Für die mittlere Flächenpressung in der Gabelbohrung gilt nach Gl.9.4: | ||
Version vom 3. Oktober 2008, 19:50 Uhr
--Bülent 17:54, 6. Sep. 2008 (CEST
Inhaltsverzeichnis
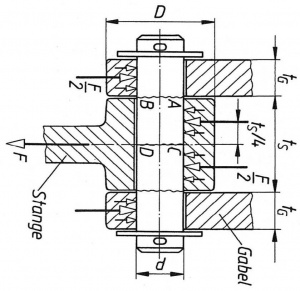
Bolzengelenk
Gegeben:
Ein Bolzengelenk wird durch eine sehr stark stoßhaft auftretende Kraft der schwellend belastet. F=14,5 kN Gabelkopf und Stange aus S275 JR,Zylinderstift nach DIN EN ISO 2338 sitzt mit einer Übermaßpassung in der Gabel und mit einer Spielpassung in der Stange.
Im Betrieb führt der Bolzen keine Gleitbewegung aus.
Gesucht:
a-) d ; ts ; tG ; l und D
b-) τmax ; τazul ; p ; pzul
c-) σb
Lösung
a-)
Einbaufall 2 liegt vor für nicht gleitende Flächen,für den der Einspannfaktor k = 1,1 beträgt.
Für sehr starke Stöße ergibt sich nach TB 3-5c der mittlere Anwendungsfaktor KA = 2,5
Für den nicht gehärteten Normstift beträgt der Rm = 400 N/ mm², bei schwellender Belastung wählt man σbzul = 0,2 *400 N/ mm².
σbzul = 0,2 *400 N/mm²
σbzul = 80 N/mm²
Der erforderliche Bolzendurchmesser wird nach Gl.9.1 bestimmt.
d ≈ k* √[( KA*Fnenn) / σbzul ] (Gl. 9.1)
Mit den angegebenen Werten und der Stangenkraft F = 14,5kN ergibt sich ein Bolzendurchmesser von
d ≈ 1,1 k* √[( 2,5*14500 N* mm²) / 80 N]
d ≈ 23,415 mm
Nach TB9-3 wird der Normdurchmesser d = 25 mm gewählt.
Stangendicke Dicke der Gabelwangen
ts ≈ 1,0 * d tG ≈ 0,5 * d TB Seite : 100 (Hinweise)
ts ≈ 1,0 * 25 mm tG ≈ 0,5 * 25 mm
ts ≈ 25 mm tG ≈ 12,5 mm
Stiftlänge
l = ts+ (2 * tG) + (2 * c)
l = 25 mm + (2 * 12,5 mm) + (2 * 4 mm)
l = 58 mm
Unter Beachtung der Fase (c) nach TB 9-3 wird der Stiftlänge
l = 60 mm gewählt.(ISO 2338-25h8*60 St) Für die Augen-(Naben-) Durchmesser gelten die unter 9.22 genannten Erfahrungswerte.
D = 2,5*d (RM 9.2.2)
D = 2,5*25mm D = 62,5mm
Das Gabelauge wird mit dem gleichen Durchmesser ausgeführt.
Ergebnis:
Als Bolzen wird ein Zylinderstift ISO 2338-25h8*60 St gewählt.Das Stangenauge wird 25mm dick, die Gabelwangen werden 12,5mm dick ausgeführt.Die Augen erhalten einen Durchmesser von 62,5mm.
b-)
Für die größte Schubspannung in der Nulllinie des Bolzens gilt nach Gl.9.3:
τmax ≈ 4/3 * [ (KA*Fnenn) / (As*2) ] < τazul (Gl.9.3)
Anwendungsfaktor KA = 2,5 wie a-)
d = 25 mm
Bolzenquerschnittsfläche As = (25² mm² *π) / 4
As = 490,87 mm²
τmax ≈ 4/3 * [ (2,5*14500 N) / (2*490,87 mm²) ]
τmax ≈ 49,23 N/ mm²
τazul = Rm * 0,15 für schwellende Belastung
τazul = 0,15 *400 N/ mm²
τazul = 60 N/ mm²
τazul = 60 N/ mm² > τmax = 49,23 N/ mm²
Für die mittlere Flächenpressung in der Gabelbohrung gilt nach Gl.9.4:
p = [(KA*Fnenn) / Aproj] < Pzul (Gl.9.4)
Aproj = Projektionsfläche zur Berechnung der mittleren Flächenpressung.
Für Gabel AprojG = 2 * d * tG
Für Stange AprojS = d * ts
AprojG = 2 * 25 mm * 12,5 mm
AprojG = 625 mm²
AprojS = 25 mm * 25 mm
AprojS = 625 mm²
p Gabel = (2,5 * 14500 N) / (625 mm²)
p Gabel = 58 N/ mm²
p Gabel = p Stange
p = [(KA*Fnenn) / Aproj] < Pzul (Gl.9.4)
Für S275JR beträgt der Rm = 430 N/ mm² (TB 1-1)
p zul = Rm* 0,25 für schwellende Belastung
p zul = 0,25 *430 N/ mm²
p zul = 107,5 N/ mm²
p zul = 107,5 N/ mm² > PGabel =58 N/ mm²
Ergebnis:
Bolzengelenk ist ausreichend bemessen, da die größte Schubspannung τazul = 60 N/ mm² > τmax = 49,23 N/ mm² und die mittlere Flächenpressung p zul = 107,5 N/ mm² > p Gabel = 58 N/ mm² ist.
c-)
Für das maximale Biegemoment im Bolzen gilt Mbmax nach Einbaufall 2:
Mbmax = (F * ts) / 8
Mbmax = (14500 N * 25 mm) / 8
Mbmax = 45312,5 Nmm
Mbmax = Mbnenn
Für die Biegespannung auf den Bolzen gilt nach Gl. 9.2 :
σb ≈ [(KA* Mbnenn) / (0,1 *d^3)] < σbzul
σb ≈ [ ( 2,5 * 45312,5 Nmm) / ( 0,1 * (25^3)mm) ]
σb ≈ 72,5 N/ mm²
σbzul = 80 N/ mm² wie a-)
σbzul = 80 N/ mm² > σb ≈ 72,5 N/ mm²
Ergebnis:
Der Bolzen ist ausreichend bemessen da die σbzul = 80 N/ mm² > σb ≈ 72,5 N/ mm² ist.
| Zurück zur Übersicht Bolzen- und Stiftverbindungen |
|---|
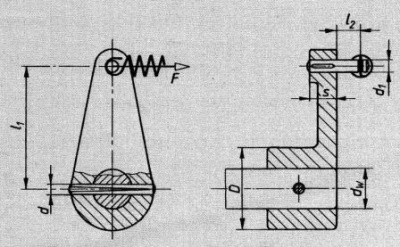
Schalthebel
Gegeben:
dw= 32mm ; F= 400 N greift schwellend an. Stöße treten nicht auf. D= 2* dw ; Kegelkerbstift nach DIN EN ISO 8744 l1 = 80mm ; Passkerbstift nach DIN 1469-C8*25-St l2= 15mm s= 12mm
Gesucht:
a-) d (mittlere) ; l (Länge) Kegelkerbstift ; Die Normbezeichnung des Kegelkerbstiftes. b-) PN ; Pw und τa (Pzul Nabe; Pzul Welle und τazul ) c-) d1= 8mm ist zu prüfen , der ggf. zu ändern ist. d-) Pmax (Pzul)
Lösung:
a-)
d = ( 0,2 … 0,3 ) * dw (9.3.2 RM)
d = 32mm * 0,25
d = 8mm
D = 2 * dw D = l
D = 2 * 32mm
D =64mm l = 64mm
Ergebnis:
Es wird ein Kerbstift ISO 8744 8 * 64 – St gewählt.
b-)
PN = [ ( KA * Tnenn ) / (d * s *( dw + s))] < Pzul ( Gl. 9.15)
S = (D – dw ) / 2 ; Tnenn = F * l1 ; KA= 1,0 keine Stöße
Tnenn = 400 N * 80mm
Tnenn = 32000 Nmm
s = (64mm – 32mm) / 2
s = 16mm
PN = (1,0 * 32000 Nmm) / ( 8mm*16mm *( 32mm+16mm) )
PN = 5,2 N/mm²
EN-GLJ-200 gilt mit Rm = 200 N/mm² (TB 1-1) Kerbfaktor = 0,7 Rm * 0,25 (Schwellender Belastung)
Pzul = 0,7 * 0,25 * 200 N/mm² = 35 N/mm²
Pzul =35 N/mm² > PN =5,2 N/mm²
Pw=[ ( 6 * KA * Tnenn) / (d * d²w)] < Pzul (Gl. 9.16)
Pw= (6 *1,0 * 32000 Nmm) / ( 8mm * 32²mm²)
Pw =23,44 N/mm²
Pzul = 0.7 * 0,25 * 400 N/mm²= 70 N/mm²
Pzul = 70 N/mm² > Pw = 23,44 N/mm²
τa = [(4 * KA * Tnenn) / ( d² * π * dw ) ] < Tazul (Gl. 9.17)
τa = (4 * 1,0 * 32000 Nmm) / ( 8² mm² *π *32mm)
τa = 19,89 N/mm²
Für den festigkeitsmäßig schwächeren Stiftwerkstoff wird mit Rm 400 N/mm² gerechnet.
Rm * 0,15 Schwellender Belastung für Tazul
Tazul= 0,7 * 0,15 * 400 N/mm² = 42 N/mm²
Tazul= 42 N/mm² > τa = 19,89 N/mm²
Ergebnis:
Die Querstiftverbindung ist ausreichend bemessen.
c-)
σb = [(KA * Mbnenn) / W] < σbzul (Gl.9.18)
Mb = F * l2 w= 0,1 *d3
Mb= 400 N * 15mm w= 0,1 * 83 mm
Mb= 6000 Nmm w = 51,2 mm3
σb = (1,0 * 6000 Nmm) / 51,2 mm3
σb = 117,18 N/mm²
Rm * 0,2 Schwellender Belastung für σbzul
σbzul = 0,7 * 0,2 * 400 N/mm² = 56 N/mm²
σbzul =56 N/mm² < σb = 117,18 N/mm²
Gewählt w= 0,1 * 123 mm
w=172,8 mm3
σb= (1,0 * 6000 Nmm) / 172,8 mm3
σb= 34,72 N/mm²
Ergebnis:
Der Passkerbstift ist zu knapp bemessen. Sicherheitshalber wird als d1=12mm gewählt.
d-)
Pmax=[( (KA * Fnenn) * (6* l +4*s) ) / (d * s²) ] < Pzul (Gl. 9.19)
Pzul = 0,7 * 0,25 * 200 N/mm² = 35 N/mm² (siehe Lösung b)
Pmax= (1,0 *400 N * ( 6 * 15mm +4 * 12mm )) / (12mm * 12² mm²)
Pmax= 31,9 N/mm²
Pzul = 35 N/mm² > Pmax= 31,9 N/mm²
Ergebnis: Die Verbindung ist ausreichend bemessen.
| Zurück zur Übersicht Bolzen- und Stiftverbindungen |
|---|