| Elastizitätsmodul | ||
|---|---|---|
| vernetzte Artikel | ||
| Streckgrenze | Stahl | |
Elastizität und Elastizitätsmodul
Elastizität ist die Eigenschaft fester Stoffe, nach einer Verformung (z.B. Verlängerung während einer Belastung auf Zug) wieder in ihren ursprünglichen Zustand überzugehen.
Der Elastizitätsmodul (kurz: E-Modul, E) beschreibt die Elastizität von Werkstoffen quantitativ ("Hookesches Gesetz"). Hierbei gilt: Je elastischer der Stoff, desto kleiner der E-Modul.
Experimentelle Bestimmung des Elastizitätsmoduls
Der Elastizitätsmodul kann über den Zugversuch experimentell bestimmt werden:
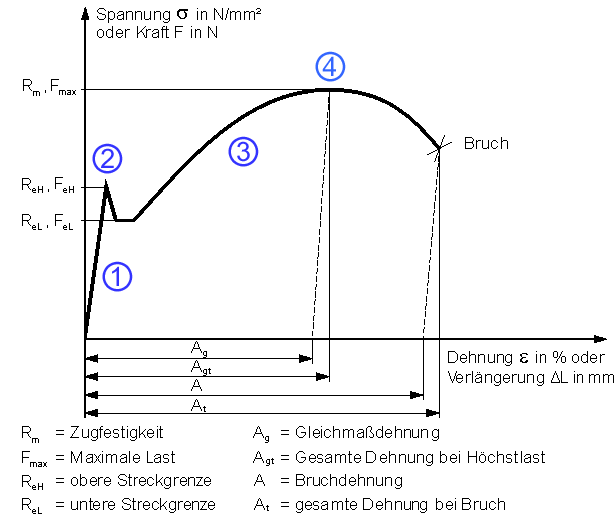
Im elastischen Bereich (siehe Spannungs-Dehnungs-Diagramm (1, Hookesche Gerade) wird das Verhältnis der Zugspannung σZ (= Zugkraft FZ pro Querschnittfläche S) zur Längsdehnung ε ermittelt, dieses Verhältnis ist der E-Modul in N/mm2 bzw. bzw. Megapascal (MPa):
| σZ · 100% FZ · L0 | ||
| E | = | ─────── = ───── |
| ε S · ΔL |
Berechnungsbeispiele
Experimentelle Bestimmung des Elastizitätsmoduls
Im Zugversuch kann der E-Modul experimentell bestimmunt werden, z. B.: Ein Probestab aus Stahl mit einer Ausgangslänge L0 von 200 mm und einer Querschnittsfläche S von 78,5 mm² wird mit einer Kraft FZ von 10.000 N auf Zug belastet. Hierbei stellt sich eine Verlängerung von 0,12 mm ein.
E = 10.000 N · 200 mm / 78,5 mm² · 0,12 mm
E = 212.314 N/mm2
Berechnung der elastischen Verlängerung eines Zugstabes
Über den E-Modul kann die elastische Verlängerung eines Bauteils berechnet werden, z. B.:
Ein Flachstahl 4 x 30 mit der Länge 2 m wird mit 18 kN auf Zug belastet. Berechne die elastische Verlängerung.
| FZ · L0 18.000 N · 2.000 mm · mm² | ||
| ΔL | = | ───── = ────────────────── = 1,4 mm |
| S · E 120 mm² · 210.000 N |
Elastizitätsmoduln
Weblinks
- Elastizitätsmodul als Google-Suchbegriff
- Elastizitätsmodul in der Wikipedia
- Elastizitätsmodul hier in bs-wiki.de mit Google
- Elastizitätsmodul als Youtube-Video
- Uni Kiel: Elastizitätsmodul in Zahlen
- Experimentelle Bestimmung des E-Moduls. Umfassende Darstellung der physikalischen Grundlagen und variantenreiche experimentelle Bestimmung des E-Moduls von David Schwarzenberg (PDF, 226 S.). Die vergleichsweise einfache Bestimmung mittels Zugversuch ist hier ab S. 60 beschrieben.