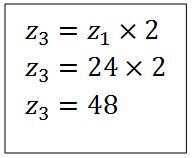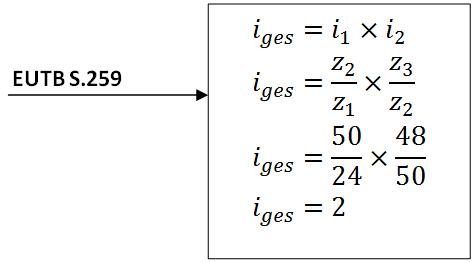Zahnräder und Zahnradgetriebe: Unterschied zwischen den Versionen
(→Aufgaben zum Rechnen) |
(→Beispielaufgabe Nockenwellenantrieb) |
||
| Zeile 250: | Zeile 250: | ||
[[Bild:Zahnräder_Nockenwellenantrieb.jpg|180px|right]] | [[Bild:Zahnräder_Nockenwellenantrieb.jpg|180px|right]] | ||
Die Nockenwelle eines Viertaktmotors dreht sich halb so schnell wie die Kurbelwelle. Sie wird durch einen Zahntrieb von der Kurbelwelle aus angetrieben. Das Zahnrad z<sub>1</sub> auf der Kurbelwelle besitzt 24 Zähne | Die Nockenwelle eines Viertaktmotors dreht sich halb so schnell wie die Kurbelwelle. Sie wird durch einen Zahntrieb von der Kurbelwelle aus angetrieben. Das Zahnrad z<sub>1</sub> auf der Kurbelwelle besitzt 24 Zähne | ||
| − | und einen Modul m= | + | und einen Modul m = 6 mm.<br /><br /> |
Wie groß muss die Zähnezahl z<sub>3</sub> des Zahnrades auf der Nockenwelle sein?<br /> | Wie groß muss die Zähnezahl z<sub>3</sub> des Zahnrades auf der Nockenwelle sein?<br /> | ||
| − | Wie groß muss die Zähnezahl des Zwischenrades sein, damit der Achsabstand | + | Wie groß muss die Zähnezahl des Zwischenrades sein, damit der Achsabstand 516 mm zwischen Kurbelwelle und Nockenwelle überbrückt wird?<br /> |
<br /> | <br /> | ||
Lösungsweg:<br /> | Lösungsweg:<br /> | ||
Version vom 11. Oktober 2008, 20:38 Uhr
Inhaltsverzeichnis |
Funktion und Wirkung
Zahnradgetriebe bestehen aus einem oder mehreren Zahnradpaaren. Es gibt geschlossene und offene Getriebe. Geschlossene Getriebe überwiegen. Zahnradgetriebe haben einen hohen Wirkungsgrad bei kompakter Bauweise.
Nachteilig ist die starre Kraftübertragung durch den Formschluss bei Getrieben (elastische Kupplungen vorsehen). Unerwünschte Schwingungen können durch bessere Verzahnungsqualität reduziert werden.
Die folgende Tabelle zeigt eine Übersicht der wichtigsten Getriebearten mit Merkmalen:
Zahnräder
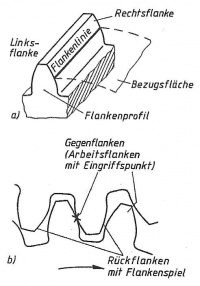
Um eine formschlüssige Kraftübertragung zwischen nicht fluchtenden Wellen zu realisieren werden Zahnräder benutzt. Jedes Zahnrad weist eine Links- und Rechsflanke auf. Entsprechend der Drehrichtung werden sie zu einer Arbeits- oder Rückflanke. Die Arbeitsflanken des treibenden und des getriebenen Zahnrades berühren sich im Eingriffspunkt (beim treibenden Rad vom Zahnfuß bis zum Zahnkopf und umgekehrt beim getriebenen Rad), wobei dieser wandert. Flankenspiel ist zwischen den Rückflanken vorhanden. Ein gegebenes Zahnrad bestimmt mit seiner Verzahnung die Verzahnung des Gegenrades.
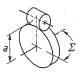
Die Funktionsfläche eines Zahnrades ist eine gedachte Fläche um die Radachse ohne Zähne. Bei einem Zahnradpaar wälzen die Funktonsflächen aufeinander ab, wenn sie die gleiche Relativbewegung machen. Die geometrischen Bestimmgrößen der Verzahnung werden auf die Bezugsfläche bezogen, welche normalerweise gleichzeitig die Funktionsfläche ist.
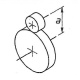
Hyperboloidräder bilden bei den Zahnradpaaren den allgemeinen Fall, von denen sich in vereinfachter Form alle Zahnradpaarungen ableiten lassen
Die Abbildung zeigt: a) Zahn mit Flankenprofil b) Arbeits- und Rückflanken
Getriebearten
Ein Zahnradgetriebe besteht aus einem oder mehreren Zahnradpaaren. In einem Getriebe wird die Drehrichtung und das Drehmoment umgewandelt. Dies kann in mehreren Getriebestufen geschehen.
Die Getriebebauarten werden nach der Lage der Radachsen bzw. der Wellen eines Zahnradpaares und der Richtung der Flanken nach DIN 868 in Wälzgetriebe und Schraubwälzgetriebe unterschieden.
Wälzgetriebe
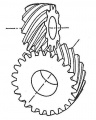
Die Wälzgetriebe unterteilen sich in Stirnradgetriebe und Kegelradgetriebe.
Allgemeines:
- In den Funktionsflächen tritt reines Wälzen auf
- Radpaare bzw. Radachsen (Wellen) in einer Ebene, also parallel oder schneiden sich (meist) im 90° Winkel
- Kontakt ist linienförmig
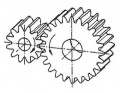
Stirnradgetriebe
- Paarung zweier außen- oder innenverzahnter Stirnräder
- Funktionsfläche ist jeweils ein Wälzzylinder
- Übersetzung je Radpaar üblicherweise i ≤ 6 (imax = 8…10)
- Sonderfall: Die Zahnstange hat einen unendlich großen Durchmesser
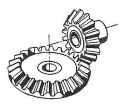
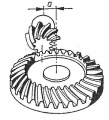
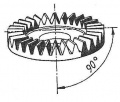
Kegelradgetriebe
- Paarung zweier Kegelräder mit Gerad- oder Schrägverzahnung
- Funktionsfläche ist ein Wälzkegel
- Übersetzung imax ≈ 6
- Berührung der Zahnflanken ist linienförmig
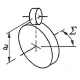
- Grenzfall ist das außenverzahnte Kegelrad = Kegelplanrad, dessen Funktionsfläche senkrecht zur Radachse (Welle) ist
Schraubwälzgetriebe
Die Schraubwälzgetriebe unterteilen sich in Stirnschraubgetriebe und Kegelradschraubgetriebe
Allgemeines:
- Radachsen (Wellen) kreuzen sich nicht in einer Ebene
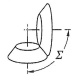
- Funktionsflächen sind Hyperboloide
- Wälzen sich bei Drehung unter gleichzeitigem Gleiten (Verschieben) längs ihrer gemeinsamen Berührungslinie aufeinander ab
- Die Verzahnungen beider Räder liegen in den hyperbolischen Funktionsflächen
- Zahnräder können als hyperbolische Stirnräder (Kehlräder) oder als hyperbolische Kegelräder ausgeführt sein
- Durch gekrümmte Funktionsflächen werden die Verzahnungen in der Praxis an Zylinder bzw. Kegelflächen angenähert
Stirnschraubgetriebe
- Die Verzahnung der Zahnräder hat Punktberührung
- Die Form wird von den Hyperboloiden an Zylinderflächen angenähert.
- Getriebe eignen sich nur für kleine Lasten imax = 5
Kegelradschraubgetriebe
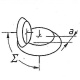
- Kleiner Achsabstand (Wellen) „a“ (z.B. Achsversatz bei Kfz-Getrieben)
- Zahnräder werden meist als bogenverzahnte Kegelschraubräder ausgeführt (werden Hypoidräder genannt)
- Bei Paarungen dieser Räder kreuzen sich vielfach die Radachsen (Wellen) rechtwinklig
- Kontakt ist linienförmig
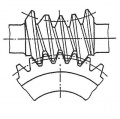
Schraubgetriebe
- Achsen (Wellen) kreuzen sich rechtwinklig
- Übersetzung von imin ≈ 5 bis imax ≈ 60 (in Ausnahmefällen bis imax ≈ 100)
- Im Eingriffsfeld besteht Linienberührung
- Zylindrische oder globoidische Funktionsflächen mit passendem Gegenrad (auch globoidisch)
Verzahnungsgesetz
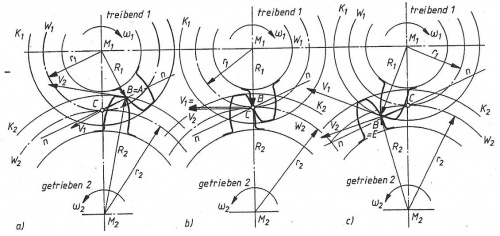
Eine konstantbleibende Übersetzung (i=ω1/ω2) ist für den gleichmäßigen Lauf des Zahnradpaares die Vorraussetzung. Als erstes berühren sich die Zähne des treibenden Rades am Zahnfuß und am getriebenen Rad am Zahnkopf im Eingriffspunkt B. Beide Zahnräder drehen sich mit den Winkelgeschwindigkeiten ω1 = treibendes Rad und ω2 = getriebenes Rad. Der Eingriffspunkt B wandert auf den Zahnflanken auf der gemeinsamen Normalen n-n. Die gemeinsame Normale n-n läuft durch den Wälzpunkt C, dies ist der Punkt an dem sich beide Wälzkreise W1 = Wälzkreis treibendes Rad und W2 = Wälzkreis getriebenes Rad berühren.
Flankenprofile und Verzahnungsarten
Zykloidenverzahnung
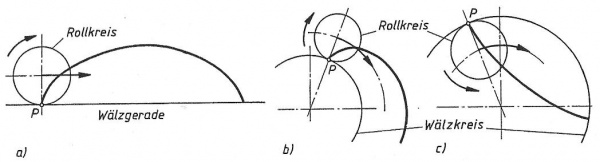
Die Zykloiden entstehen durch das Abrollen eines Rollkreises auf einer Wälzgeraden (a) eine Orthozykloide). Die Wälzgerade kann auch rund sein und heißt dann Wälzkreis. Der Rollkreis kann außen ( b) eine Epizykloide) oder innen ( c) eine Hypozykloide) auf dem Wälzkreis abrollen und so eine Zykloide erzeugen.
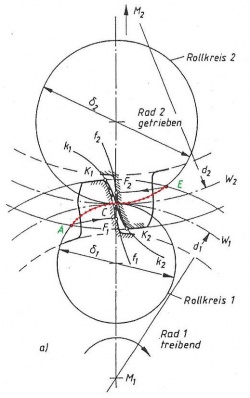
Die Eingrifflinie setzt sich zusammen aus den Bögen der Rollkreise (Bild a)). Die Eingriffsstrecke, gepunktet (rot) dargestellt, beginnt im Punkt A und endet im Punkt E.
Gleichzeitig, neben einer Wälzbewegung, erfolgt noch eine Gleitbewegung, die aus den unterschiedlichen Längen hervor geht.
Bei diesem Verzahnungstyp ist immer ein konvex gekrümmtes Flankenprofil mit einem konkav gekrümten Flankenprofil im Eingriff. Die Flächenpressung ist durch günstiges Anschmiegen der Zahnflanken aneinander geringer, dadurch gibt es weniger Abnutzung und die Belastbarkeit der Zahnräder steigt.
Bei der Zykloidenverzahnung ist es möglich Zahnräder mit kleinen Zähnezahlen herzustellen (z=3).
Da die Verzahnung immer aus dem Zusammenspiel von zwei Zahnrädern entsteht, gehören diese als Satz zusammen. Möchte man Wechselräder oder Schieberäder realisieren, geht dies nur unter Verwendung gleicher Rollkreise.
Die Zykloidenverzahnung wird nur in Sondergebieten eingesetzt, da ihre Herstellung sehr teuer und schwierig ist. Die Herstellwerkzeuge haben keine geraden Schneidkanten. Die Einsatzgebiete sind z.B. die Feinwerktechnik.
Treibstockverzahnung
Die Triebstockverzahnung ist eine spezielle Form der Zykloidenverzahnung. Durch diese Form entsteht eine Punktverzahnung. Um die Abnutzung zu reduzieren wird der Punkt mit dem Durchmesser dB vergrößert. Das Ritzel wird an die Triebstockbolzen angepasst.
Anwendungsgebiete sind z.B. Krandrehwerke und Karussels. Bei ihnen sind große Übersetzungen vorhanden.
Evolventenverzahnung
Eine Kreisevolvente wird mit einem Grundkreis und einer Rollgeraden konstruiert. Auf dem Grundkreis wird die Rollgerade abgerollt. Die Bahn, die der Startpunkt beschreibt, ist die Kreisevolvente. In dem Bild kann man die verschiedenen Zwischenpunkte 1 bis 6 sehen. Die Rollgerade ist dabei immer tangential zum Mittelpunkt des Rollkreises.
Bei der Evolventenverzahnung gibt es an jedem Zahn zwei Teile von Kreisevolventen, die den Zahn bilden (rot markiert im Bild20-12b). Die Eingriffslinie ist nach dem Verzahnungsgesetz eine Gerade n-n. Sie berührt die beiden Grundkreise tangential zu den Mittelpunkten der Räder, in den Punkten T1 und T2. Der Punkt C liegt auf dem Punkt, wo sich beide Wälzkreise berühren auf der gedachten Linie zwischen den Mittelpunkten der Zahnräder M1 und M2. Wenn man im Punkt C eine Linie im 90° Winkel zeichnet, erhält man die Linie t-t. Der kleine Winkel zwischen den Linien M1-M2 und t-t ist der Eingriffswinkel α. Der Winkel α findet sich auch noch an anderen Stellen im Bild wieder (blau markiert).
Die Linie, die entsteht, wenn zwei Zahnflanken anfangen sich zu berühren, bis zu dem Punkt, wo sie sich nicht mehr berühren, ist die Eingriffslinie. Sie ist abhängig von der Drehrichtung der Zahnräder. Im Bild a) ist die rot gepunktete Linie für die angegebene Drehrichtung und die gestrichelte für den umgekehrten Drehsinn eingezeichnet.
Die Evolventenverzahnung ist, weil ihre Eingriffslinie eine Gerade ist, unempfindlich gegen Achsabstandsänderungen.
Die Verzahnung bei Hohlrädern ist konkav. Im Bild 20-13b kann man einen Teil eines Hohlrad sehen. Die Eingriffsstrecke ist rot markiert.
Zahnräder sollten möglichst eine Zähnezahldifferenz von z2-z1 ≤ 10 Zähnen haben. Bei geringerer Zähnezahldifferenz (bei einem Übersetzungsverhältnis nahe i=1) kann es zu Zahnüberschneidungen kommen.
Anwendung der Evolventenverzahnung ist im Maschinenbau, dort wird sie fast ausschließlich verwendet. Die Zahnräder können kostengünstig und relativ einfach hergestellt werden.
Bezugsprofil, Herstellung der Evolventenverzahnung
- Bezugsprofil eines Stirnrades ist nach DIN 867 ein festgelegtes Profil mit geraden Flanken
- Bezugsprofil ist durch den Modul mn festgelegt (mn = 1…70mm)
- Rad und Gegenrad haben gleiches Bezugsprofil
- Der Kopfkreis des Zahnrades wird durch Verzahnungswerkzeuge nicht bearbeitet
Zahnradwerkstoffe
Es kommen bei Zahnrädern folgende Werkstoffe zum Einsatz:
- Gusseisen mit Lamellengraphit
- Gusseisen mit Kugelgraphit
- Schwarzer Temperguss
- Stahlguss
- Stähle
Stähle haben die größte Bedeutung. Bei gleichen Werkstoffpaarungen besteht Fressgefahr.
Schmierung der Zahnradgetriebe
Text
Getriebewirkungsgrad
Der Gesamtwirkungsgrad setzt sich aus den einzelnen Wirkungsgraden für Lagerung, Dichtung und Verzahnung zusammen.
Verzahnungswirkungsgrade:
| Gerad-Stirngetriebe | ηZ bis 0,99 |
| Kegelradgetriebe | ηZ bis 0,98 |
| Stirnradschraubgetriebe | ηZ ≈ 0,50 … 0,95 |
| Schneckengetriebe | ηZ ≈ 0,20 … 0,97 |
Die Wirkungsgrade der schrägverzahnten Stirnradgetriebe sind ca. 1-2% kleiner gegenüber einer Geradverzahnung.
Aufgaben zum Rechnen
Die Aufgaben zum Berechnen wurden mit dem Europa Tabellenbuch 43. Auflage berechnt. Die Abkürzung "EUTB S..." bezieht sich auf diese Ausgabe. In anderen Ausgaben können die Seitenzahlen abweichen.
Beispielaufgabe Nockenwellenantrieb
Die Nockenwelle eines Viertaktmotors dreht sich halb so schnell wie die Kurbelwelle. Sie wird durch einen Zahntrieb von der Kurbelwelle aus angetrieben. Das Zahnrad z1 auf der Kurbelwelle besitzt 24 Zähne
und einen Modul m = 6 mm.
Wie groß muss die Zähnezahl z3 des Zahnrades auf der Nockenwelle sein?
Wie groß muss die Zähnezahl des Zwischenrades sein, damit der Achsabstand 516 mm zwischen Kurbelwelle und Nockenwelle überbrückt wird?
Lösungsweg:
gegeben: a/b) z1 = 24 ; m = 6mm ; a = 516mm
gesucht: a) z3 = ?
a) Die Kurbelwelle muß 2 Umdrehungen machen, wenn die Nockenwelle eine Umdrehung ausführt, d.h.:
Für das Zahnrad z3sind 48 Zähne ermittelt.
b) Berechnung Teilkreisdurchmesser d1 und d3
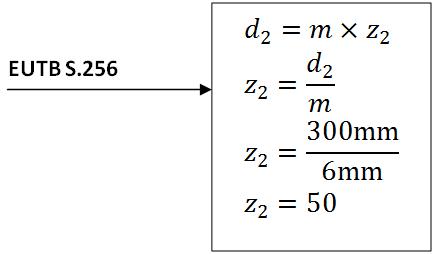
Mit den ermittelten Durchmesser kann man nun den Teilkreisdurchmesser des Zahnrades d2wie folgt ermitteln.
Mit dem ermittelten Teilkreisdurchmesser d2 kann man nun unter zu Hilfenahme des Moduls die Zähneanzal des Zahnrades berechnen.
Mit der ermittelten Zähnezahl z2 überprüft man nur noch einmal das Übersetzungsverhältnis.
Das Zahnrad z2 hat 50 Zähne. Gesamtübersetzung ist iges=2. Bei einem Zwischenrad egal wie groß es ist kann das Übersetzungsverhältnis i=z3/z1 ermittelt werden.
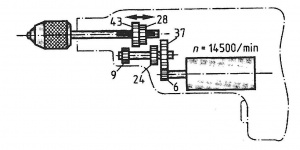
Zweigang-Bohrmaschine
Für die abgebildete Bohrmaschine sollen folgende Werte berechnet werden:
Die Drehzahlen der Bohrspindel
Die Schnittgeschwindigkeit bei einem Bohrerdurchmesser von 10mm bei niederster Drehzahl.
hier gehts zur Lösung
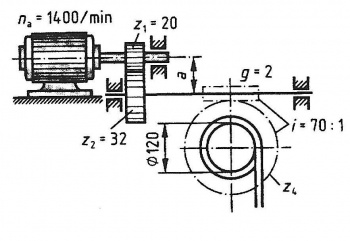
Seiltrommelantrieb
Für den Seiltrommelantrieb müssen folgende Berechnungen durchgeführt werden:
a) Die Drehfrequenz der Schnecke
b) Die Drehfrequenz der Seiltrommel
c) Die Geschwindigkeit des Seiles in m/s
d) Den Achsabstand a bei Modul m = 4mm
e) Die Zähnezahl des Schneckenrades z4
hier gehts zur Lösung
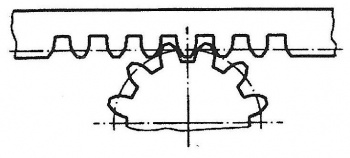
Zahnstangenantrieb
Eine Zahnstange wird durch ein Zahnrad mit z = 32 angetrieben. Modul m = 4mm.
Wie groß ist der Hub der Zahnstange bei einer Zahnradumdrehung?
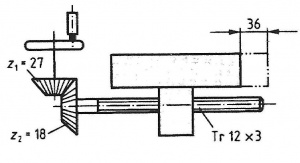
Tischverstellung
Ein Tisch einer Maschine kann wie in der Abbildung verstellt werden. Berechnen Sie:
a) Die Zahl der Kurbelumdrehungen für einen Weg von 36 mm
b) Den Weg bei einer Umdrehung der Kurbel.
Übersetzung
Ein Elektromotor treibt über ein zweistufiges Zahnradgetriebe eine Säge an. Die Motor-drehfrequenz ist 1440 min-1, die Säge hat eine Drehfrequenz von 192 min-1. Die Zahnräder der ersten Stufe haben z1 = 18 und z2 = 45 Zähne. Das Zahnrad z4 hat 42 Zähne.
Berechnen Sie:
a) Die Gesamtübersetzung
b) Die Einzelübersetzungen
c) Die Zähnezahl des Zahnrades z3
Literatur
Diese Bücher haben mir bei der Lösung vieler Probleme geholfen:

|
Roloff/Matek Maschinenelemente, Lehrbuch und Tabellenbuch Vieweg Verlag 18.Auflage 2007 ISBN 978-3-8348-0262-0, Preis € 36,90 |

|
Roloff/Matek Maschinenelemente, Formelsammlung Vieweg Verlag 9.Auflage 2008 ISBN 978-3-8348-0534-8, Preis € 20,90 |

|
Roloff/Matek Maschinenelemente, Aufgabensammlung Vieweg Verlag 14.Auflage 2007 ISBN 978-3-8348-0340-5 , Preis € 26,00 |

|
Alfred Böge Handbuch Maschinenbau Vieweg Verlag 18.Auflage 2007 ISBN 978-3-8348-0110-4 , Preis € 69,90 |

|
Tabellenbuch Metall Europa Lehrmittel Verlag 44.Auflage 2008 ISBN 978-3-8085-1724-6 , Preis € 23,80 |

|
Schierbock Formeln und Tabellen für metalltechnische Berufe Bildungsverlag eins 17.Auflage 2007 ISBN 978-3-8239-7140-5 , Preis € 13,80 |

|
Hoischen/Hesser Technisches Zeichnen Cornelsen Verlag 31.Auflage 2008 ISBN 978-3-589-24130-9 , Preis € 21,00 |

|
Dubbel Taschenbuch für den Maschinenbau Springer Verlag 22.Auflage 2007 ISBN 978-3-540-49714-1 , Preis € 79,95 |
--Timewarper 12:20, 8. Dez 2007 (CET)
--Timewarper 12:11, 15. Dez 2007 (CET)